Egy újítás hihetetlen hódítása
Arabok-e az arab számok?
Míg a világ nyelveinek írásán több tucat kisebb-nagyobb írásmód osztozik ma is, addig a számjegyek írását szinte teljes mértékben a magyarul arab számok néven ismert számjegyek uralják. Korábban azonban nagyon sok írásnak saját jelölése volt a számokra is. Hogyan, hol és mikor alakultak ki, illetve minek köszönhető az arab számjegyek átütő sikere?
Az „arab”számjegyek valójában nem az araboknál alakultak ki, hanem Indiában, és az írás elterjedéséhez képest viszonylag későn. A sumerek és az egyiptomiak is nagyjából az i.e. 3. évezred közepétől már használtak írást, és a számokat is jelölték. A következő 3000 évben népek tucatjai vették át tőlük, vagy alakították ki saját írásmódjukat és számjegyek jeleit, de a ma használt számjegyek története valójában csak i.sz. 500 körül kezdődött Indiában. Természetesen a babiloni, a görög, a római és a kínai matematikusok és csillagászok is használtak számokat, de az áttörő változást csak a számok helyi érték alapú lejegyzése hozta meg.
Al-Hvárizmi szobra Üzbegisztánban.
(Forrás: wikimedia commons / Euyasik)
A helyi érték alkalmazásának különlegessége, hogy radikálisan leegyszerűsíti a matematikai műveletek végrehajtását, ami e nélkül folyamatos bonyolult átalakításokat és átszámításokat kíván. A római számokkal is lehet például szorozni és összeadni, de ehhez a jelölt számokat „konkretizálni” kellett, például abakusz segítségével. (ilyesféle eszközöket már ősidők óta ismertek). A jól működő helyi érték alapú matematika feltétele pedig a nulla, de nemcsak a nulla (latin nullus, ’semmi’) fogalma, hanem annak jelölése is.
Az oldal az ajánló után folytatódik...
A zéró fogalmáról már a fent említett kultúrákban is tudtak, de rendszeres jelölése sosem terjedt el. A maják ugyan már i.e. 36-tól használtak jelölést a nullára, ez viszont akkor nem jutott, nem juthatott el az óvilágba. Indiában azonban már legalább valamikor az i.sz. 5. századtól elkezdték használni a nulla tízes számrendszer szerinti helyi értéki jelölését. Indiai matematikusok dolgozták ki a nulla alapvető algebrai és aritmetikai alkalmazását is (Brahmagupta, 628). Az indiai számokat és használatukat vette át a perzsa származású Abu Abdalláh Muhammad ibn Músza al-Hvárizmi (i.sz. 780 – 845).
Al-Hvárizmi Bagdadban élt és arab nyelven írta műveit. Bagdadban jelent meg A Számítás hindu számokkal című munkája is 825 körül, és ezzel az „arab” számok visszafordíthatatlanul elindultak hódítóútjukon. Nevéhez nemcsak ez, hanem az algebra és az algoritmus szavak származása is köthető, az előbbi egyik könyvcímének, az utóbbi pedig saját nevének rövidítéséből és latinosításából került be az európai nyelvekbe az első latin nyelvű fordítás után (1145). Maga a zéró szó szintén arab eredetű, a صفر ṣifr, ’üres’ szó olasz változata honosult meg különböző módokon az európai nyelvekben. (Az arab kifejezés egyébként pedig a szanszkrit sunya fordítása.)
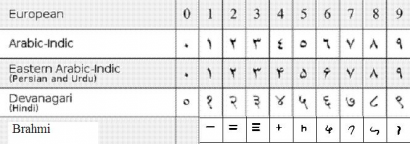
A nagyon jó kulturális kapcsolatokkal rendelkező arab világ tudósai között gyorsan terjedt az új számjelölés, a távolsággal és az idővel azonban kicsit megváltoztak a számok formái. A hindu-arab számokként is ismert jelöléseknek három fontosabb változata létezik ma is: az indiai, a keleti arab és a nyugati arab. Európába e legutóbbi érkezett el, melyeket a 976-os kiadású Codex Vigilanus említ először.
Lentről felfelé: bráhmi (i.sz. 100), dévanágari, perzsa, keleti arab és nyugati számjegyek.
(Forrás: wikimedia commons, nyest)
Az új számjegyek európai meghonosodása lassú folyamat volt. A következő lökést a számjegyeket Észak-Afrikában elsajátító olasz matematikus, Leonardo Fibonacci 1202-ben kiadott Liber Abaci című könyve adta, de az általános elterjedés csak a nyomatatás feltalálása után – Gutenberg, c. 1440 – gyorsult fel. Angliában például 1445-ben, Magyarországon pedig V. László (1440-1457) rövid uralkodásának végén jelentek meg az arab számok először. Oroszország a 18. század végén, Nagy Péter uralkodása alatt, Kína és Japán pedig a 19. század végén kezdte el használni az arab számjegyeket. Ma már szinte minden ország és nyelv alapvetően a hindu-arab számokat használja, azoknak is túlnyomórészt az általunk is ismert nyugati arab változatát. Ez alól kivételt csak azok a nyelvterületek képeznek, ahonnan a nyugati arab számok korábbi változata történelmileg származik, tehát főleg az arab országok és India kulturális hatókörzete.
Ez utóbbi területhez főleg Dél-Ázsia és Délkelet-Ázsia tartozik, ahol sok nyelv a bráhmi családba tartozó saját írásmódot használ. Az indiai nyelveken kívül ilyen még például a burmai, a thai, a lao, és a khmer is. Ezek a nyelvek nem csak bráhmi írásra visszavezethető írásjelekkel rendelkeznek, de többségüknek saját, a hindu-arabhoz hasonló, helyi érték alapú számjegyeik is vannak. Ugyan ma már az európai számjegyek is általánosan ismertek ezeken a területeken is, de a hagyományos helyi számjegyek használta is él még. Például e nyelvek wikipédia szócikkei is gyakran a hagyományos számjegyeket használják, és a bankjegyek előlapján is gyakran találkozhatunk ilyen európaiak számára „felismerhetetlen" számokkal.
Vajon milyen számot takar ez az egyiptomi bankjegy?
(Forrás: wikimedia commons)
A hindi nyelvű wikipédia is a dévanágari számokat használja, de az indiai bankjegyeken már csak a nyugati arab számok jelennek meg, pont azért, mert az indiai nyelvek többségének saját számjegyei vannak. A dévanágari számjegyekkel is találkozhatunk azért bankjegyeken, például a nepáli rúpiákon.
Az arab világban a számjegyek használata nem teljesen egységes. Egyiptomtól nyugatra az Európában is ismert nyugati arab számjegyek jellemzőek, a többi területen viszont a keleti arab számjegyek az általánosan elterjedtek. Ez a különbség az térség bankjegyeinek számjegyeiben is megmutatkozik. A keleti arab államok papírpénzének előlapján a keleti arab számjegyek szerepelnek, és csak a hátoldalukon láthatóak az európaiak számára is könnyen felismerhető nyugati arab számjegyek, míg Egyiptomtól nyugatra már a bankjegyeken is csak az utóbbi számokkal találkozhatunk.
A fent említett példák ellenére az arab számjegyek sikere szinte teljesnek mondható, és alapvetően a logikusságuknak, praktikusságuknak köszönhető.
Olvasói kérésre itt egy táblázat a számjegyek európai fejlődéséről:
Források:
http://mathforum.org/dr.math/faq/faq.roman.html#calc
http://www.omniglot.com/language/numerals.htm
http://www.skypoint.com/members/waltzmn/Mathematics.html
Hozzászólások (121):
Követem a cikkhozzászólásokat (RSS)
1
peterbodo
2011. március 11. 09:56
Ha jól emlékszem a szifr (0) szóból származik a magyar cifra szó, az akkoriban alkalmazott karikás díszítések miatt.
+1 kérdés: A 14. században Magyarországon is úgy írták a 4-et, mint a fenti táblázat dévenágari változata. Gondolom nem közvetlen átvételről volt szó. Ekkor még az arabban is ilyen volt, vagy nálunk alakult vissza véletlenül olyanra, mint az eredeti?
2
El Mexicano
2011. március 11. 10:10
3
takacs janos
2011. március 11. 10:38
Valahol azt olvastam, hogy Dürer alakította ki a mai "arab" számokat. Mivel ezek olyannyira különböznek a nyugati arab számoktó ill. a második sorban lévő Arabic-Indic számoktól, helyesebb lenne Dürer számokról beszélni és nem arab számokról. Egy arab kollégám csodálkozik is azon, hogy a számainkat arabnak hívjuk, mert azok annyira különböznek az ő számaiktól.
4
anokó
2011. március 11. 10:47
A cikk második mondata tárgyi tévedés. Jelenlegi tudásunk szerint a folyamközbe időszámításunk előtt 3250 körül betelepedett egy népcsoport, amely intellektuálisan magas szinten állt. Fejlett matematikájuk volt. A tízes és hatvanas számrendszer kombinációját használták. Ez a népcsoport használta először a kör 360 fokos felosztását. Ezek használata eléggé magas szintű matematikai tudást feltételez. Ma már azt is tudjuk, hogy ez a népcsoport a ős szkíták voltak. Ezt a népcsoportot Julius Oppert (1825-1905) zsidó származású asszirológus 1859. évi munkájában nevezte el " sumer" -nak. Ez a népcsoport alkalmazta először az ékírást is.
A cikk konklúzióját sajnos nem igazán értem. A számjegyek számértékeket reprezentálnak . Milyen logikai rendet vél ön felfedezni az arabnak vélt számjegyek megjelenésében?
5
ppeli.geo
2011. március 11. 11:03
@peterbodo: Igen, a cifra szavunk is innen származik, akárcsak több európai nyelv szava a számjegyre, és még az angol cipher szó is:
* The French formed the word “chiffre” and adopted the Italian word “zero”.
* The English used “zero” for “0”, and “cipher” from the word “ciphering” as a means of computing.
* The Germans used the words “Ziffer” (digit) and “Chiffre”.
* The Dutch still use the word "cijfer" to refer to a number.
* The Italians also use the word "cifra" to refer to a number.
(wikipedia)
+1 kérdésre:
A cikk végén frisstítésként elhelyezett táblázatból látszik, hogy a számjegyek fokozatosan nyerték el végső formájukat.
6
ppeli.geo
2011. március 11. 11:14
7
ppeli.geo
2011. március 11. 13:45
@anokó: Legjobb tudásom szerint fejlett matematikájuk ellenére a sumérok nem használták még a zérót. Babilóni matematikusok, akik átvették a sumér rendszert, i.e. 300-tól használtak egy jelölést a nullára, de ez sem volt teljes értelemben helyi értékű jelölés.
A záró kérdésre csak ismételni tudom a cikk második bekezdését:
„A helyi érték alkalmazásának különlegessége, hogy radikálisan leegyszerűsíti a matematikai műveletek végrehajtását, ami e nélkül folyamatos bonyolult átalakításokat és átszámításokat kíván. A római számokkal is lehet például szorozni és összeadni, de ehhez a jelölt számokat „konkretizálni” kellett, például abakusz segítségével. (ilyesféle eszközöket már ősidők óta ismertek). A jól működő helyi érték alapú matematika feltétele pedig a nulla, de nemcsak a nulla (latin nullus, „semmi”) fogalma, hanem annak jelölése is.”
8
anokó
2011. március 11. 14:28
@ppeli.geo:
Az ős szkíták (sumerok) a zérót nem ismerhették. A cikk tartalmazza a zéró szó vélhető eredetét.
Ismerték azonban a fogalmi jelentését , kezdőpontnak , vagy középpontnak tekintették. A kör 360 fokos felosztása sokkal magasabb szintű matematikát feltételez, mint a nulla fogalmi jelentése és gyakorlati használata.
9
Fejes László (nyest.hu)
2011. március 11. 16:07
@anokó: A szkíták sztyeppei iráni népek voltak, a sumérok Babilóniában éltek, nyelvük szigetnyelv. Semmiféle kapcsolatuk nem bizonyított.
Annak, hogy a kört hány fokra osztják fel, semmi jelentősége nincs. mivel jobb a 360, mint a 100 vagy az 1?
10
anokó
2011. március 11. 17:56
@Fejes László (nyest.hu):
Nem szeretnék nyelvészeti vitába bonyolódni. Remélem van arról információja, hogy a folyamközben fellelt ékírásos agyagtáblákat már a múlt század közepén megfejtették. Azokban elolvasható információk vannak, amelyek alátámasztják azt amit leírtam. Babilon akkád elnevezés, amely az ős szkíta Báb-ili , Báb-iláni , Babilla névalakból alakult ki. Akkád jelentése " az istenek kapuja". A babiloni központtal kialakuló Babilónia jelentős birodalommá csak i.e.24.század után fejlődött már szemita uralom alatt.
Amire hivatkoztam az a folyamköz ősnépe amely i.e.3250 körül telepedett le, és már akkor magas intellektuális szinten állt. Ekkor a területen még nem éltek szemita népek.
Annak hogy a kört hány fokra osztják fel , annak geometriai, térképészeti és matematikai jelentősége van , nem is elhanyagolható mértékben.
11
anokó
2011. március 11. 18:28
@Fejes László (nyest.hu):
A múlt századot " pontosítanám " !
Miután 1844-ben Henry Rawlinson ( 1810-1895) angol katona-diplomata lemásolta a háromnyelvű behisztumi sziklafelíratot, majd Georg F. Grotefend (1775-1853) német középiskolai tanár megfejtette azt, csak akkor sikerült a babiloni ékírás és nyelv megfejtése. A megfejtéshez az ó-perzsa felíratok adták meg a kulcsot. A babiloni nyelv megfejtése után tudták csak megfejteni az asszír ékírást és nyelvet. Csak ezek után vált lehetővé az ős szkíta (sumer) ékírás és nyelv megfejtése.
12
tenegri
2011. március 11. 18:57
@anokó: "Nem szeretnék nyelvészeti vitába bonyolódni."
Pedig szerintem itt nyugodtan meg lehet ezt tenni, bár kétségtelen, hogy nem kifejezetten kapcsolódik ehhez a cikkhez.
"Azokban elolvasható információk vannak, amelyek alátámasztják azt amit leírtam."
Mármint azt, hogy a sumérok és a szkíták egy és ugyanaz? Mint pl.?
Az összes többi leírt dolog szép, csupán csak semmi köze ahhoz, hogy szkíták lennének a sumérok. A szkíta nyelvekről nem túl sok konkrét adat van, de azok alapján iráninak tűnnek, plusz közvetett adatok is erre utalnak (pl. uráli és altaji nyelvek iráni jövevényszavai). A sumérről viszont sokkal több forrás van, s még ha a pontos hangalakok és a kiejtés meglehetősen homályos is helyenként, de a rendszer elég egyértelmű, s ez alapján nagyon nem hasonlít a szkíta nyelvemlékekre.
13
Fejes László (nyest.hu)
2011. március 11. 19:16
@anokó: Csatlakoznék tenegrihez, plusz egy kérdés: "Annak hogy a kört hány fokra osztják fel , annak geometriai, térképészeti és matematikai jelentősége van , nem is elhanyagolható mértékben." -- Mi?
14
tenegri
2011. március 11. 19:28
@anokó: "Annak hogy a kört hány fokra osztják fel , annak geometriai, térképészeti és matematikai jelentősége van , nem is elhanyagolható mértékben."
Bizonyára éppen ezért nem ezt a rendszert használják a térképészettel vagy matematikával foglalkozó szakemberek, hanem leginkább a radiánt :) A 360-as fokfelosztás csak bonyolítja a számításokat, így inkább mellőzni szokták az általános- és középiskolán kívül.
15
anokó
2011. március 12. 08:03
@tenegri:
Olyan kérdésekben, hogy a tyúk vagy a tojás volt-e előbb nincs értelme vitatkozni.
A radián, vagy ívmérték csak 1873 óta használatos . A térképészet még ma is a háromszögelés elvét használja , mert egyenes távolságot zsinórral, mérőszalaggal vagy optikai mérőműszerekkel pontosan lehet mérni. A radiánhoz mint ívmértékhez átszámítás szükséges és talán a " pi " ismerete. A földgömböt is kézbe vehetnéd megnézni, hogy mi a francnak használták a 360 fokos felosztást? Vagy miért is kilencven fok a derékszög?
16
anokó
2011. március 12. 08:28
@tenegri:
Okos ember lehetett ez a Julius Oppert ! Az ékírásnak 16 féle tipúsát ismerte. Nemcsak a " sumer " elnevezés, de az ékírásnak a keilschrift és az écriture de cuneiforme elnevezés is az ő nevéhez fűződik.
Nagy valószínűséggel tudta, hogy mit csinál, amikor a következőket mondta: " Az ékírást nem a semiták , tehát nem is az asszírok találták fel. Egy semita nyelv kifejezésére az ékírás - szótagoló jellege folytán - nem igazán megfelelő. Az asszír jelek hangértékei egyébként sincsenek a legcsekélyebb vonatkozással sem a jelek képi jelentéseire." Oppert az írás feltalálását a scytháknak ( szkítáknak ) tulajdonította, amit a kor vezető tudósai , Lenormant, Rawlinson, Sayse és végül Hinks is elfogadott. Oppert háromféle scythát különböztetett meg: méd-scytha, kasdo-scytha és ős- scytha. Ez utóbbit ez utóbbit nevezte sumer-nak.
17
tenegri
2011. március 12. 09:21
@anokó: "Olyan kérdésekben, hogy a tyúk vagy a tojás volt-e előbb nincs értelme vitatkozni." Jó, bár nem tudom mire gondoltál ezzel.
"A radián, vagy ívmérték csak 1873 óta használatos . A térképészet még ma is a háromszögelés elvét használja , mert egyenes távolságot zsinórral, mérőszalaggal vagy optikai mérőműszerekkel pontosan lehet mérni. A radiánhoz mint ívmértékhez átszámítás szükséges és talán a " pi " ismerete."
Mi köze mindennek a 360 fokos felosztáshoz? Már miért kellene átszámolni bármibe is a radiánt? Csak azért, hogy fok legyen belőle?
"A földgömböt is kézbe vehetnéd megnézni, hogy mi a francnak használták a 360 fokos felosztást?"
Hagyományból, s nem azért, mert ennek különösebb jelentősége van. Ugyanúgy lehetne a 360 fok helyett 100 vagy 50 vagy 8000 vagy 792 is. A triviálisnál bonyolultabb matematikai számításokban a bizonyos szempontú egyszerűsége miatt mégis a radiánt használják.
"Vagy miért is kilencven fok a derékszög?"
Mert a 360 foknak a negyede - fokban számolva. Radiánban a derékszög PI/2, gradiánban meg 100 - semmi lényegi különbség.
Az, hogy a sumérok 360 részre osztották a kört, nem azért fontos és jelentős, mert pont 360 részre osztották, hanem azért mert egyáltalán foglalkoztak vele, hogy felosszák, s olyan matematikai számításokat végeztek, amelyeknél már felmerült az igény erre.
18
tenegri
2011. március 12. 09:28
@anokó: A sumér nyelv és kultúra felfedezésekor azt sok mindennel próbálták rokonítani, párhuzamba vonni. A sumér nyelvet a világ szinte összes szóba jöhető nyelvével összevetették, s végül az jött ki, hogy egyikkel sem tűnik rokoníthatónak. Ha te most leragadsz a 150 évvel ezelőtti számos próbákozás egyikénél, figyelmen kívül hagyva, hogy azóta ezek egyike sem bizonyosodott be, az nem tűnik valami okos dolognak. Amiket pedig eddig leírtál, azoknak az ég világon semmi közük hozzá, hogy a szkítákkal akarod összehozni a sumérokat, abszolút semmilyen összefüggésben nincsenek ezzel. Senki nem vont kétségbe semmit az ékírás sumér eredetével, sémi és indoeurópai nyelvekra történt alkalmazásával vagy kutatástörténetével kapcsolatban.
19
anokó
2011. március 12. 09:38
@tenegri:
Az ős szkítákat sajnos nem áll módunkban megkérdezni, hogy miért osztották fel a kört 360 részre, azt sem tudjuk megkérdezni, hogy ismerték- e a pi-t . Azt viszont megpróbálhatjuk elképzelni, hogyan rajzolhattak kört középpont nélkül, és hogyan számolták meg az év napjainak számát.
Ez olyan mint amikor ész érveket ütköztetünk eszetlen érvekkel. Jobban megvilágítva a kérdést Az ész érv értelmes betűkombináció, a ZeromorphemX pedig nem az. A vitához közös nyelv kell, amelyet mindketten értünk. A vitáért magáért én nem vitatkozom.
20
anokó
2011. március 12. 09:48
@tenegri:
Amikor J.Oppertet megkérdezték, hogy miért nevezte el a folyamköz ősnépét és nyelvét " sumer " nak a következő választ adta. : " A régi babiloni uralkodók sumer és akkád királyainak nevezték magukat. Akkád annak a vidéknek a földrajzi neve volt, amelyet sémiták laktak. Sumer,Babilonia nem sémita lakosságú vidékének elnevezése. Ezért Babilonia nem sémita lakosságát sumeroknak, nyelvüket pedig sumer nyelvnek nevezhetjük." A további vitát vele próbáld lefolytatni, ha ezt a kérdést nyelvészeti kérdésnek tekinted!
21
Fejes László (nyest.hu)
2011. március 12. 11:00
@anokó: "Azt viszont megpróbálhatjuk elképzelni, hogyan rajzolhattak kört középpont nélkül, és hogyan számolták meg az év napjainak számát." -- Mi köze a 360-nak a középponthoz? Az évről meg valamelyik nagyokos honvédelmi miniszterünk jut eszembe, aki 365 fokos körkörös védelemről beszélt...
22
Fejes László (nyest.hu)
2011. március 12. 11:01
@anokó: Az, hogy a sumérok magukat nem nevezték suméroknak, azt bizonyítja, hogy szkíták voltak? Különben kronológiailag legfeljebb az jöhetne szóba, hogy a sumérokból lettek a szkíták, és nem fordítva...
23
tenegri
2011. március 12. 11:58
@anokó: Ennek már megint mi köze a szkítákhoz? Nem látom a megállapításaid és az azok alátámasztásaként felhozott érveid közötti összefüggést.
24
anokó
2011. március 12. 12:19
@Fejes László (nyest.hu):
Böszmeségre sem vagyok hajlandó böszmeséggel válaszolni.
Annyi tiszteletet J. Oppert talán megérdemelne, hogy ne csináljunk belőle hülyét.
Abban 100 százalékban igaza van, hogy a folyamköz ősnépe magát sumernek soha nem nevezte.
Azonban nem ez bizonyítja, ős szkíta mivoltukat, hanem az 1880 ban feltárt tellói leletek, amelyek ma a Louwre féltve őrzött kincsei.
A telloi leletekről szóló todományos leírásokat az Akademie Francaise csak 1882- ben hozta nyilvánosságra. Tehát minden kétséget kizáró módon bebizonyosodott, hogy a folyamközben az igen korai időkben már i.e. negyedik évezredben élt egy ragozó nyelvet beszélő nép, ez pedig az ős szkíta volt, amelyet J.Oppert 1859- ben átkeresztelt sumer- nak.
Az ős szkíta sumer kontinuitás tehát igaznak bizonyult. A sumer ős szkíta kontinuitás ezért nem létező fogalom. ( kontinuitás = folytonosság)
25
anokó
2011. március 12. 12:21
@tenegri: Sajnos mi nem egy nyelvet beszélünk.
26
elhe taifin
2011. március 12. 12:42
@anokó:
Honnan lehet tudni, hogy a sumerok magukat szkítának nevezték? Milyen korabeli források tudósítanak erről?
27
Fejes László (nyest.hu)
2011. március 12. 13:19
@anokó: Bocsássa meg böszmeségemet, de mi az a Louwre? És mi az az Akademie Francaise
Komolyra fordítva a szót: pontosan melyik lelet és hogyan bizonyítja a sumérok és szkíták azonosságát? www.google.com/search?q=tello+site:louvre.fr Hogyan tudják az elődöktől származó leletek bizonyítani, hogy kik lesznek majd az ő leszármazottaik?
És még mindig érdekel, hogy mi köze a kör középpontjának a 360 fokhoz, továbbá hogy milyen előnyökkel jár, ha éppen 360 fokra osztjuk fel a kört...
28
anokó
2011. március 12. 13:49
@elhe taifin:
Ön valamit nagyon félreértett ! Amit állítottam az a következő: Az ős szkíták magukat soha nem, nevezték sumer-nak.
29
elhe taifin
2011. március 12. 13:57
@anokó: Azt én értem, csak azt nem értem, hogy ez a szkíta elnevezés min alapul.... (Lásd Fejes László hozzászólását)
30
anokó
2011. március 12. 14:30
@Fejes László (nyest.hu):
Bocs, hogy a forrásanyagból betű szerint másoltam le a Louvre és a Francia Akadémia szavakat.
Folyamatosan az ős szkítákra hivatkoztam megjelölve forrásként J.Oppert asszírológust. Ön pedig a szkítákról beszél, akik sokkal később tűntek fel a történelem színpadán . Már J. Oppert is háromféle szkítát említ, valószínűleg nem véletlenül.
A körrel kapcsolatos kérdéseire is szívesen válaszolok. A válaszom a kérdés második felére vonatkozik.
Földünk a nap körül nem egészen pontosan 365,25 nap alatt tesz meg egy kört ( elliptikus pályán) Ezt már az ős időkben megszámolták ( megmérték) . Ennek a számnak nagyon sok egész számú osztója nincs.
Most következik az előny!
360:1=360
360:2=180
360:3=120
360:4=90
360:5=72
360:6=60
360:7=51,4286
360:8=45
360:9=40
360:10=36
360:12=30
Figyelmébe ajánlanám a hetes számot, amely különleges státuszt kapott .
Az a ciklus, amelyet mi hétnek nevezünk és napjait hétfő, kedd,szerda,csütörtök, péntek, szombat, vasárnap napelnevezéssekkel illetünk azért lett bevezetve,mert lehetővé teszi a 365 napos napév és a tényleges 365,25 napos év összehangolását. Ez a " továbbgördülés titka"
31
anokó
2011. március 12. 14:36
@elhe taifin:
Kérdését megpróbálom J.Opperthez továbbítani. A válasz megérkezésekor jelentkezem.
32
elhe taifin
2011. március 12. 14:59
34
najahuha
2011. augusztus 13. 17:10
Nagyon sok ősmúltbéli tisztázandó dolog van.
Többek között a MÉTER .
A történészek kevésbé figyeltek azokra az összetevőkre, amelyek alapján már 200 évvel korábbra vonatkozóan is kimutathatóak a méter hosszúságának ma használatos ismérvei. Nem is beszélve arról, hogy valójában 6000 éves múltra tekint vissza.....
Csakhogy a MÉTER az ősidőkben KÖRMÉRETET jelentett , ezért nincs sehol "méterrúd"......Helyette viszont ismertek a könyök és kettősláb rudak...
Egyiptomban például az ÉSZAKI LÁB (31,6 cm) ÁTMÉRŐVEL képzett kör kerülete kb. 1 Méter
Az ÉSZAKI LÁB és a MÉTER ugyanazon nevezetes kör két ősi meghatározója.
Ahány ÉSZAKI LÁB az átmérő, annyi MÉTER bármely kör kerülete.
Tehát 3 északi láb átmérőjű kör kerülete 3 méter.
Miért fontos ez ?
Mert így NEM KELLETT a PI-vel számolni.
A métert zsínórral/kötéllel mérték.
Egyiptomi ábrázolása magáért beszél. kis kör, aláhúzva.
A sumérok is ismerték a hosszingát, így bármikor létre tudták hozni az egységes hosszmértéket. Az általuk megalkotott hosszmérték egysége mai értékben : 99,88 cm.
A 60, 360 mint fölosztási rendszer egyfajta legkisebb közös többszörösként került bevezetésre.
A két legfontosabb sumér számot, a 360 és a 366-ot összeköti a PI és a FI kombinációja.
Ismerték a négyzetgyökvonást, leírták a Marduk (Jupiter) sebességváltozatait egy táblázatban, ők írták le először az ekliptikát, a Nap látszólagos pályáját a csillagok között.
Ez a számszaki felosztás önmagát adta.
35
Krizsa
2013. január 31. 19:40
@anokó: Na végre. És a pi számot is ismerték, (8/9)x(8/9) = 3.2 közelítéssel.
Nulla pedig egyáltalán nem kell a nagyságrend váltáshoz,
csak akkor, ha a számjelek egyesével mind különbözőek.
Ehelyett:
. **** fölötte vízszintes vonal: 5,
ugyanez, plusz még egyszer négy pont **** és mellette álló vonal: 10.
Ilyen számlálás látható a 30.000 éves francia barlangrajzokon.
A zero SZÓ - a latinba - a héberből került bele. S a héberbe? Az már nyilván még korábbi sémi nyelv(ek)ből.
A héber zar'ón = mag, zéra = ondó, zaáruri = parányi. visszajutottunk a magyar ZÁR szóhoz.
Ez a még ősibb szó, az európai kárpátnyelv (szubsztrátnyelv) korából.
A zéro őseink tudatában nem lehetett az "üres halmaz számossága", mert ilyesmit az ősember nem ötölhetett ki.
Ami olyan kis helyre van beZÁRva, hogy nem is látszik, mégis ember / platánfa, stb. lesz belőle, az zéro állapotban van.
EZT már tudhatta még az ősember is.
Tehát szerintem nem a sifra a zéró, hanem az csak a "szám" szónak az eredete.
-**********
A magyar cifra
A héber cipor = madár (ált. kicsi, délvidéken jellemzően szinesebb), cfirá = koszorú (köralakú), cipóren = köröm (az is köralakú), tollhegy (eredetileg valódi toll), szegfű (cifra).
MIÉRT a héber (vagyis afro-sémi eredet helyes a latinnal szemben? Mert a latin a magyar nyelvhez képest nagyon fiatalka:-).
36
Krizsa
2013. február 1. 06:48
És a pi számot is ismerték, (8/9)x(8/9) = 3.2 közelítéssel. Lemaradt a 4-es szorzó.
Helyesen (8/9)x(8/9)x4 = 3.2.
37
anokó
2013. február 1. 09:35
@Krizsa: Már-már sajnálom a szerencsétlen finnbugrisokat, amikor lealázod őket, most viszont vitatkoznék veled. A 8/9 -es arányszámot nem a folyamközben használták, hanem Egyiptomban. A kör területének kiszámításához az alábbi megoldóképletet használták: A (kör terület)= dxd x (8/9) x (8/9) ahol d= a kör átmérője.
38
Krizsa
2013. február 1. 10:39
Én úgy tudom, hogy mindkét helyen használták a pi számot, s a suméroknak volt kicsit gyengébb a közelítése a 3.14-hez.
S hogy a kiszámítás módjában eltérés volt közöttük.
Valójában csak azt akartam érzékeltetni, hogy a tudományok már a suméroknál is olyan magas szinten voltak, am itökéletesen KIZÁRJA, hogy az Özönvíz előtt ne lett volna hasonló. De NEMHOGY kevesebb, hanem vagy ugyanolyan, vagy még előrehaladottabb kultúra, tudomány kellett legyen. Na hallod, ekkora, 100%-os pusztulás után!.
Azt is felteszem, hogy pont ugyanott, Mezopotámiában volt "régi-Suméria". Csak az kb. 3000 évre tenger, majd mocsárvidékké vált. Miért gondolom, hogy pont Mezopotámiában volt "régi-Suméria" is? Azért mert a halott korszak alatt pont a környékén támadtak a nagykultúrák. Ez mutat arra, hogy legalábbis a "fejekben" sok minden át lett mentve.
Mezopotámiából ugyan még egy sas se menekülhetett el, de mindig vannak távollevők, küldöttek, kereskedők stb.
*********
Itt jöhet be - esetleg - a "sumér-magyar", valójában az európai szubsztrátnyelv rokonsága.
De nem Sumériából, hanem a 8-10.000 évnél is régebbi elő-kultúrából. Annak a részben elfelejtett, részben töredékesen előre-hátra ragasztott szótagjaiból álló újabb nyelvekben.
Tegnap nézegettem vagy 2 órát az itt ajánlott internetes sumér szótárt. Jegyezgettem is... kb. 300 szónak az angol fordítását. A "mintamondatokat" is hozzáolvastam.
Egyértelmű véleményem: a sumér nyelv még töredékesen is csak alig van megfejtve.
Megindokolom: a legeslegegyszerűbb szavakra tömegesen,
elfogadhatatlanul sok szóváltozatot ad a szótár.
Pl. a víz-re. A víz ősi, genetikusan beírt értelme a fejünkben (szerintem) vit-, visz. Egy nyelvben lehet egy olyan gyöke a víznek, ami egészen más? Persze. Nem baj, ha nem látok kapcsolatot. Lehet kettő is? Ez is az én bajom. Habár azért kell legyen valami "vit-, visz FONETIKÁJÚ szó is... a legtöbb nyelvben van.
De 5-6 féle vízfogalom, a különböző példamondatokkal? ez csak a fordítás bizonytalansága, a vízfogalom be-nem-azonosítása lehet abban a nyelvben.
Ha egy ilyen jelenség van: nem számít. Ha 20, az sem.
De ezt a "fordításbőséget" én tegnap kb. 200 nagyon-alapfogalomra találtam hasonlónak.
Másik megérzésem: a sumér, részben, talán 20%-ban szintén sémi alapú. Harmadik, s ez biztos: valóban ragozó nyelv is.
A magyar is ilyen.
S ettől még nem magyar a sumér? Hát nem.
De finn mégkevésbé:-))))))).
39
anokó
2013. február 1. 11:42
@Krizsa: A folyamközben kialakult magas kultúra tagjai magukat sohasem nevezték sumernek. A Nyesten is olvasható volt erről egy anyag, amely megvilágítja a dolog hátterét. Az első szemita csavar volt a cikk címe. Abban egyetértek veled, hogy már a folyamközben kialakult magas kultúra előtt volt a földön magas kultúra, amely a mostani tudásszintünket is meghaladhatta.
40
szigetva
2013. február 1. 11:48
@anokó: „a mostani tudásszintünket is meghaladhatta” és minden nyom nélkül eltűnt?
41
Krizsa
2013. február 1. 11:56
Nem, hanem a Sumériának nevezett kultúra szinvonalát - vagy elérte, s talán meg is haladta már az epusztult mezopotámai kultúrája. Így értettem.
Mert olyan NEM LÉTEZIK, hogy Suméria, Óegyiptom, az indus és perzsa kultúrák csak úgy a semmiből ugrottak volna elő. Mivel semmiféle "primítivebb" előzményüket nem találtak sehol - Ez tökéletesen kizárt dolog.
42
tenegri
2013. február 1. 12:09
@Krizsa: " Mivel semmiféle "primítivebb" előzményüket nem találtak sehol - Ez tökéletesen kizárt dolog"
Csak én látok ebben ellentmondást? Ha nem találtak "primitívebb" előzményt, az miért is utalna rá, vagy pláne bizonyítaná, hogy volt "fejlettebb" előzmény? Főleg, hogy a "primitívebb" bizonyára kevesebb felfedezhető nyomot hagy, mint egy "fejlettebb", s ez utóbbit ennek ellenére nem találtak. Abba nem mennék bele, hogy mit fognak még találni vagy nem találni és hol, s mi volt és mi nem volt, csak épp az általad feldobott okból sehogy sem következik a megállapított okozat.
43
Krizsa
2013. február 1. 12:14
A Gyöknyelvészet címú könyvem 939. oldaláról:
"Sumér. A sumérok önmagukat KINGIR-nek hívták. A héber kín = sirat, gyászol, gár = lakik, gir = mészkő. Sumérnak csak a hódító akkádok nevezték őket - éspedig a pikkelyes díszítésű tárgyaik után.
A héber samúr = órzött. Ez a szó szlovákul ponyot jelent, s a pontyot valóban a pikkelyei őrzik"
Vesd össze: smaragd (színes korund), smirgli, sömör (pikkelyes bőrbetegség).
44
anokó
2013. február 1. 12:33
@szigetva: A meghaladhatta, jelzi, hogy feltételezésről van szó! Nem tűnt el nyomtalanul. A folyamközbe betelepült ősszkíták már készen hozták magukkal a magas műveltséget, de jelenleg nem tudjuk, hogy honnan érkeztek. Ezt a tudást tekintjük jelenlegi kultúránk alapjának.
45
anokó
2013. február 1. 12:38
@Krizsa: A KINGIR szónak egy más megfejtése is lehet! A KING jelenthet királyt is. A hosszú magánhangzóval az Ír az Írás alkalmazását sejteti. A királyi-szkíták írástudásáról pedig tudunk.
46
Krizsa
2013. február 1. 13:13
Nem vállalok felelősséget a kingír-ért, mert valszeg a Wikiből vettem.
A sumér szavak tegnapi átböngészéséből sem azt a tanulságot vontam le, hogy a sumér egy sémi nyelv, hanem csak azt, hogy már az afro-sémivel is bekevert nyelv. Egyidőben azt is láttam, hogy a mellette levő akkád szavak nagyobb arányban "sémibbek".
Mégis: a sumér szótagírás teszi kevéssé valószínűvé a KING szófejtést. Miért? Mert a szótagoknak - a gyöknyelvészet alapján - különálló értelmeket érdemes keresnünk.
47
anokó
2013. február 1. 13:55
@Krizsa: A gyöknyelvészethez nem tudok hozzászólni. Annyit azért tudok, hogy a magyar nyelvben a legrövidebb szó jelentését is a szövegkörnyezete egyértelműsíti. Ez a szabály elég régen része lehet a magyar nyelvnek. Ez azonban kétségessé teszi a rendszered általánosítását. Kérdés: Szerinted arabok-e az arabnak vélt számok?
48
szigetva
2013. február 1. 14:02
@anokó: „a mostani tudásszintünket is meghaladhatta”, „Nem tűnt el nyomtalanul” Az ember a holdon járt a múlt században. Milyen nyomok maradtak, amik arra utalnak, hogy ezt bármikor korábban meghaladhatta az emberiség?
@anokó: „A KING jelenthet királyt is.” Csakhogy erről a sumerek mit sem tudhattak.
@anokó: @Krizsa: Bájos, hogy komolyan azt képzelitek, releváns véleményt tudtok alkotni „a sumér szavak tegnapi átböngészéséből” olyan kérdésekben, amiről más több éves, évtizedes munka után mond valamit.
49
Krizsa
2013. február 1. 14:15
@anokó: "...a legrövidebb szó jelentését is a szövegkörnyezete egyértelműsíti."
Például?
A mostani számjegyek nem. A "leronokítási" táblázat sem eléggé meggyőző.
A magyar számrendszer egyértelműen
10-es alapú volt, "ameddig a szem ellát".
A 30.000 éves francia barlangrajzokon pont-vesszős NAGY számok vannak.
A héber és az arab betűszámokat használ. A vallásos héberek ma is. A betűszámoknak szó-értelmük is van, tehát nyilvánvaló, hogy mindenhol előbb volt a számot reprezentáló egyszerű fogalom (pl. öt újj).
50
anokó
2013. február 1. 16:05
@szigetva: Releváns véleményt csak azokról a hozzászólókról tudok mondani, akik tényként kezelnek feltételezéseken alapuló megállapításokat. Én nem böngészek sumér szavakat, mert olyanok nincsenek! Sumérnek nevezett szavak azonban vannak, de azokat sem böngészem. A meghaladhatta, lehetett szavak azt jelzik, hogy ezeket nem tényként közlöm, csak feltételezem. " Nem tűnt el nyomtalanul" Nem tudom, mit tanultál az iskolában, de ha ezt kérdezed, mindaz amit tanultál eltűnt nyomtalanul. Jelenlegi kultúránk alapja az a tudás, aminek semmi nyoma nem maradt, de a folyamközben 5250 évvel ezelőtt már megvolt.
51
anokó
2013. február 1. 16:19
@Krizsa: Az el szócska jelentését adom példának: Eladhattad volna, El betűvel kell írni, El jöhettetek volna, El számolhatnál velem, Elhelyezkedhetnél a ranglétrán, Elhízol, ha sokat eszel, Elvetemült voltál, Korán elmentél,pedig későn feküdtünk le, El feküdt a búza a nagy esőben. Sorolhatnám a végtelenségig, Mit is jelent az el szócska? A magyar számrendszer tízes alapú volt amióta világ a világ . Egyetértek veled! Az hogy előtte mi volt nem tudjuk, de magyar nyelv az biztosan nem.
52
szigetva
2013. február 1. 16:21
@anokó: Ezt feltételezed: „a mostani tudásszintünket is meghaladhatta.” De még mindig nem mutattál semmit, amire egy ilyen feltételezést alapozni lehetne. Hogy ki tudták számolni a kör kerületét, az nem haladja meg „mostani tudásszintünket”, azt még én is ki tudom számolni. Egyébként ha tényleg meghaladta, akkor azt talán mi fel sem ismernénk, ugye?
53
anokó
2013. február 1. 16:49
@szigetva: A mi technikai civilizációnk ma képtelen lenne elszállítani és helyére emelni egy 1200 tonnás kőtömböt. Az előző magas kultúra ezt meg tudta tenni. Meg tudod magyarázni, hogy hogyan tehették?
54
szigetva
2013. február 1. 16:57
@anokó: Nem, de elég sok elméletet láttam már erről. Egyébként azt se tudom megmagyarázni, hogyan építették az Øresund-hidat.
55
anokó
2013. február 1. 17:24
@szigetva: Az elég szomorú, hogy egy hidat nem tudnál felépíteni, Hogyan hoznál létre egy egyetemes nyelvet? Ez csak tréfa volt. Sok minden van amit még nem tudunk megmagyarázni, de feltételezéseket tehetünk, amelyek megvitathatóak. Ez viheti előre az egészet.
56
Krizsa
2013. február 1. 20:49
@anokó: Hát a legrövidebbekét tényleg a szövegkörnyezet adja meg, mert azok az egyetlen magánhangzóból álló indulatszavak "igésítései":
a! (a, az) e! e (e, ez) ó! ő, ú! (de mivel az ö, ü kifejezetten újkori hangok, ősi, "eredeti" jelentéseket nem keresgélek velük)
Ezek az egy hangból álló indulatszavak a legrégibb J igeképzővel a magyarban: aj ej! ój uj! - még mindig indulatszavakat adnak.
A most használatos L kozmopolita igeképzővel már olyasmit jelentenek, hogy:
lent, arra, rá csinál valamit: al-,
"felfelé-zik": ál-,
innen "máshová-zik", ált. mozogni képes: el-, él,
fölötte van, rápasszol: il-,
állandó jelleggel csinál valamit: ol-,
befejezte azt a valamit, véglegesség, úgy maradás: ul-
A L ma is használatos párja az R igeképző,
ami általában (de nem mindig) "rosszabbra fordítja a dolgot". Vagyis ilyen értelmeket ad:
ar-, ár (elárasztja), er-, ér (erre, eléri) , ir-, ír (belehatol),
or- (beborítja - bár védheti is), ur- (uralja vagy elemészti: fény / tűz)
Milyen nyelvekben vannak ezek az értelmek? A magyarban és / vagy a héberben biztos, mert megvizsgáltam. A többi általam ismert nyelvben nem végeztem RENDSZERES kutatást - mondjuk csak az az összélményem, hogy hasonlóképpen.
De ha önálló, vagy biztosan előragként megjelenő szócskáknak
a fentiektől nagyon eltérő értelmeit ismered, bármilyen nyelvben, szóljál.
******
Egyszóval az EL példával igazad van, csak te az emberi beszédnek pont a legősibb értelmeihez nyúltál vissza.
57
Krizsa
2013. február 1. 21:03
@anokó: "...magyar nyelv az biztosan nem."
Az európai szubsztrátnyelvet,
az előtt az általam KÁRPÁTNYELV-nek nevezett beszédkészséget (sűrű bocsánatot kérek, hogy magyarnak találtam születni - dehát igazából nem is ettől függ. Rudabánya, Heidelberg, Vértesszőlős - mi másnak nevezzem?)
Istenem, hát mégse hívták még "magyarnak" az ősembert?... kár... de már belenyugodtam valahogy.
58
anokó
2013. február 2. 10:37
@Krizsa: " Hát a legrövidebbekét tényleg a szövegkörnyezet adja meg" Megnyugtatlak, hogy ez a szabály nem csak a legrövidebbekre érvényes! Ez a magyar nyelvben egy általános érvényű szabály. "mert azok az egyetlen magánhangzóból álló indulatszavak " igésítései" " A magyar nyelvben több-száz kétbetűs szó van, ezeknek csak kis része indulatszó. " csak te az emberi beszédnek pont a legősibb értelmeihez nyúltál vissza." Ez azért nem teljesen így van! Én a magyar nyelv L betűjének fonetikus hangértékéhez ( el ) nyúltam vissza. Azt hittem ismered a magyar nyelv titkát. Nálunk az L (el) rejti a titkot is. Az előzőekben elfogadtad azt, hogy magyar nyelv azóta van mióta világ a világ. Azelőtt a mindenséget nem nagyvilágnak hívták. Én azt állítom, hogy az emberi beszéd legősibb értelmeihez kevés eséllyel tudunk visszanyúlni.
59
Krizsa
2013. február 2. 11:39
A többi mássalhangzó nem kozmopolita igeképző.
A legősibbnek feltételezett a T hang. Mivel zöngétlen, és mivel a beszédkezdetkor a kisbabák egy sor T-vel rokon, de későbbi mássalhangzót ejtenek T, Ty-vel (genetika), már az előember hangjai közé tartozott. Pl.: atajok (akarok, tyeleti (szereti), topok(dobog), tyotye (sose), stb. A babanyelvben megjelennek a hangváltozások legrégibb hangjai. Ez is genetika:-)
Az XT (X bármilyen magánhangzó) értelme a mai magyarban:
hat, hatásos. De a magánangzóval kezdődő mai szavak, feltételezésem szerint, eredetileg egy lágy H-val kezdődtek. Ez H a magyar szavakban nem mindenhol esett le.
Az XT általános névmás, eredeti, ősi értelme: az egész külvilágból mindazt jelentette, ami hatással lehetett az ÉN-re.
Magyar gyökszavai: át, ét(el), óta-utó (idő), öt (ujj, karom), őt, út, üt.
Héber gyökszavai: át = lecsapott rá, rávetette magát,
ata = jön (arám), ote = betakarta, ati = miatta, et = ásó,
ata = most, mostantól, tehát, iti = ideiglenes, et = idő, időszak
ata, at = te, iti, ito = velem, vele, oti, oto = engem(et), őt
ET = tárgyrag, -val, -vel.
Bármelyik mássalhangzóval végigvezetem neked a hasonló sort, mindkét nyelvben, ha érdekel.
60
Krizsa
2013. február 2. 11:56
Persze, ha az L további ősi értelmeire vagy kíváncsi, akkor van még az LX gyök.
Magyar gyökszavai: le-, le! (vele), lé, ló, lő.
Héber előragként: lx- = ra-, -nak, -hoz, -ig, -ni (főnévi igenév képző)
laá = lenyelte, loa = garat, kráter, la! = ne!, nem
li = nekem, lo, la = őneki, lu = ha, bárcsak.
S mivel tudom rokonítani a magyar LÓ szót? Azt a héberből csak az XL gyökből: ole = felszáll. De erre már kereshetsz más, kevésbé ősi eredetet is...
61
Varmer
2013. február 3. 17:22
@anokó: Te trollkodsz szegény Krizsával.
62
anokó
2013. február 4. 12:47
@Varmer: Mire alapozod az állításodat? Én közöltem a Krizsával, hogy nem tudok hozzászólni a gyöknyelvészethez. Nem minősítettem a hozzászólásait, mert nem ismerem a gyöknyelvészetet.
63
Diczkó
2013. április 26. 14:59
Üdvözlök mindenkit!
Én úgy látom, a székely rovás magánhangzókészlete nagyjából fedi az arab számjegyeket. (mássalhangzós rendszerre való áttéréskor felmaradhatott, és hogy ne menjen pocsékba, számjelölésre hasznosíthatták)
A sorrend egytől kilencig a következő:
I E É Á A O Ü U Ö
64
Diczkó
2013. április 26. 15:06
@Fejes László (nyest.hu):
"Az évről meg valamelyik nagyokos honvédelmi miniszterünk jut eszembe, aki 365 fokos körkörös védelemről beszélt..."
- Ebben már a maligánfok is benne van.
65
Diczkó
2013. május 14. 22:38
@anokó:
"... továbbgördülés titka"
@najahuha:
"... a 360 és a 366-ot összeköti a PI és a FI kombinációja."
Ezek elég titokzatosan hangzanak. Gondolom, rajtam kívül mindenki érti. Nem úgy a CIFRA szónak és változatainak az eredetét, ami egy betűrejtvény. Mondanám és mutatnám ha a rendszer engedne képet feltenni.
A MÉTERhez annyit, hogy a MÉR szó a MER, MERÍT szavak hatására lett. Eredetileg folyadék, ömlesztett áru térfogatának mérését jelentette. A mért mennyiség fogalmára a MÉRET, vagy a MERÍTÉK szót használták, v.ö. görög METRON, METRIKOSZ. Innen terjedt tovább.
66
szigetva
2013. május 14. 23:02
@Diczkó: Forrás? Vagy te találtad ezt ki?
67
Diczkó
2013. május 15. 08:33
@szigetva:
Köszönöm az érdeklődésed, de sajnos nem tudok válaszolni. (Meghaladja a képességeimet.)-: Még csak azt sem mondhatom, hogy szerénységem tiltja, hogy a forrást megnevezzem. Biztosan voltak, vannak olyan kutató-író emberek (pl. Magyar Adorján), akik ezt az ordító összefüggést már dokumentálták.
68
kisbuddha
2018. április 11. 12:26
@Diczkó: Keressetek rá Kolumbán Sándorra. Talán volt itt is egy cikk róla, hogy mennyire légből kapott zagyvaság, amiket összeír az ilyet "a világ összes nyelve magyarul van" témában.
69
Diczkó
2018. április 12. 00:41
@kisbuddha:
A METRIKO - MÉRTÉK azonosságot először talán Dr. Aczél József jegyezte le az Ősgörög eredetünk és a kun-szittya nyelv című 1924-ben Veszprémben megjelent könyvében.
70
szigetva
2018. április 12. 01:32
@Diczkó: Azonosság? A TR vs RT? A szerkezet meg akkor nyilván azonos a szekreterrel, Sok ilyen hülyeséget lehet idézni (Karthágó=Kard hágó), de nem érdemes.
71
Túlképzett Tanyasi Troll
2018. április 12. 13:26
@szigetva: A mérték meg a metric azonossága nyilván hülyeség (akár a kun-szittya-magyar nyelvrokonság), de azért ne tegyünk úgy, mintha hasonló jelenség (metatézis: hangsorrend-csere szavakon, pontosabban azok leszármazottain belül) elvileg általában is teljesen ismeretlen vagy képtelenség lenne:
pl. lat. miraculum > ósp. miraclo ~ miraglo > sp. milagro
lat. parabola > ósp. parabla > sp. palabra
72
Diczkó
2018. április 12. 21:34
@szigetva:
Így van. Engem megszólítottak, erre reflektáltam. Te pedig a saját hülyeségeidet jobb, ha magadban tartod.
73
szigetva
2018. április 15. 15:17
@Diczkó: Igen, csak nem vetted észre, hogy a [metriko] meg a [mérték] távolról sem "azonos". Ezt azonosságnak nevezni hülyeség. Nem kell megsértődnöd ezen, nem téged neveztelek hülyének, hanem azt, amit ideírtál.
Olyasmi lehet, hogy az IEu me- 'mér' és a mai magyar [mér] őse összefügg, ennek most nem fogok utánanézni, de te nem ezt írtad.
74
Sultanus Constantinus
2018. április 16. 09:45
@Túlképzett Tanyasi Troll: A spanyolban a szonoránsok egyébként is nagyon szeretik a hangátvetést, számos példát lehetne még hozni (sibilare > *siblar > silbar, veneris > *vienres > viernes).
A milagro egyébként félművelt eredetű szó, szájhagyomány útján *mirajo lett volna (vö. oculu > ojo, *veculu [< vetulum] > viejo).
A -c'l-, -g'l-, -li- eléggé furcsán fejlődött a spanyolban: [lj] > [zs] > [s] > [ch] (ez az, ami a spanyolban teljesen egyedi az újlatin nyelvek között, hogy a vulgáris latin [lj]-ből lett kezdetben [zs], de a [j] meg [j] maradt).
75
El Vaquero
2018. április 16. 16:18
Érdekes cikk, nekem anno kimaradt. Nem tudtam, hogy Indiából származnak ezek a számok. Bár az összehasonlító táblázatokból nekem az jön le, hogy amiket a világ használ ma már, azok sem nem hindi, sem nem arab számok, hanem európai számjegyek. Valóban van hasonlóság a számjegyek között, de csak a 0-1 és 9 esetén, a többi nem is hasonlít az arabbal, a hindivel meg végképp nem. Így szerintem a hindiből és az arabból nem a számjegyek jöttek (vagyis azok is, csak átalakultak), hanem a helyiértékes jelölés. Egyébként nekem úgy tűnik, hogy nem csak az „arab” számok, de a latin betűs írás is elterjedt. Már sok éve is ha az ember vett egy PC-s alaplapot, akkor a japán részhez lapozva arra lehetett figyelmes, hogy krix-krax, még több krix-krax, Pentium 4, krix-krax, DDR, krix krax, stb.. Pedig ahogy olvastam, az távol-keleti ázsiai világban a kínai típusú krix-krax írások terjedtek el, mert kulturálisan felsőbbrendűnek tartják a számukra túl egyszerűnek tűnő latin betűs írásnál.
Ami engem mindig is foglalkoztatott, hogy lenne-e értelme átállni a nyugati világban 10-es számrendszerről 2-esre. Szerintem csak bonyolítaná a lejegyzést, túl hosszúak lennének az akkora számok, mint az évszámok, meg csak mindenki tévesztené a túl hasonló számjegyeket.
76
szigetva
2018. április 16. 17:33
@El Vaquero: Ha jobban megnézed, több hasonlóságot is felfedezhetsz. A 2, 3 csak el van forgatva, a 4 nincs összekötve, az 5-nek nincs teteje. Az "A" se hasonlít az "a"-ra, vagy az "R" az "r"-re, de azért tudjuk, hogy az utóbbiak az előbbiből módosultak.
Nyilván nem lehet áttérni a bináris számokra, de miért is kellene? (Mellesleg a 12-esre se lehet, pedig annak több értelme volna (a 3-mal osztható "kerek" számok pl.).
77
Túlképzett Tanyasi Troll
2018. április 16. 17:33
@El Vaquero: Ami miatt most ez a cikk újra "trending" lett, az a következő aranyos, politikai töltetű szösszenet: mno.hu/belfold/kiakadtak-a-pecsiek-nem-a...rab-szamokat-2458948 A fő üzenete persze az, hogy „az emberek hülyék, lám, még azt sem tudják, hogy mi arab számokat használunk, ezek szavaztak a Fideszre annyian stb.” (Figyelmen kívül hagyva, hogy mekkorát szívnánk azzal, ha a mostani arab számjegyeket vezetnénk be újonnan.)
Szerintem a nyugati emberek számára egyáltalán nem érné meg 2-es számrendszerre átállni. Azokon kívül, amit mondtál, a 10-es számrendszerre épül az általunk jól ismert SI-metrikus rendszer is (jó, angolkák persze itt is kivételek); felnőttként baromi nehéz lenne átállni valami másra, mint amit ismerünk; tíz ujjunk van a kezünkön, ami kényelmessé teszi a decimális számrendszert a manuális számításoknál, számolástanulásnál; bináris rendszerre átállva kénytelenek lennénk hosszú számokat használni a bankjegyeken (20 000 forint > 100111000100000 forint) stb.
Azokat az előnyöket, amelyekkel a kettes számrendszer rendelkezik, ki tudjuk használni a számoló- és számítógépek használatán keresztül is (igaz, nekik így muszáj oda-vissza konvertálni, ha humanoidokkal kommunikálnak, de ez a kapacitásaikba bőven belefér).
78
Mackósajt
2018. április 16. 18:00
@El Vaquero: "Pedig ahogy olvastam, az távol-keleti ázsiai világban a kínai típusú krix-krax írások terjedtek el, mert kulturálisan felsőbbrendűnek tartják a számukra túl egyszerűnek tűnő latin betűs írásnál."
Azok az országok, amelyek most használják a kínai írás valamilyen formáját hivatalosan (Kínán kívül gyakorlatilag Korea és Japán, de a koreai módosított jeleket használ), nagyon sok idővel az európai írás érkezése előtt bevezették azt, és a sajátjukká vált. Szó sincs arról, hogy a kínai és az európai írás nagyjából egyszerre érkezett volna, és választottak volna köztük.
Plusz: Vietnamban a korábban nem egyedüliként, de széles körben használt kínai írást éppenséggel kiszorította a latin betűs írás a 20. század során.
Plusz: a japánok az európai írás megismerése előtt kifejlesztettek maguknak saját hangjelölő írásokat, mivel a kínai írás önmagában alkalmatlan volt a nyelvük leírására. Ezek a hangjelölő írások nem különösebben cirkalmasak a latin ábécéhez képest.
Úgyhogy nem tudom hol olvastad, de pontosításra szorul.
79
aphelion
2018. április 16. 18:59
@El Vaquero: A 2es számrendszer nagyon elnyújtja a számokat, úgyhogy konkrétan azt kb semmilyen kontextusban sem érdemes, viszont helyette a 16os vagy 8as számrendszer adott esetben praktikus lehet bizonyos alkalmazásokra (informatikában használgatjuk is őket). Arra viszont, hogy a 10es helyett általánosan áttérjenek a népek a mondjuk 16osra........hát eléggé nulla, avagy arab eredetű szóval élve zérus az esély.
80
arafuraferi
2018. április 16. 21:00
@El Vaquero: "Ami engem mindig is foglalkoztatott, hogy lenne-e értelme átállni a nyugati világban 10-es számrendszerről 2-esre. Szerintem csak bonyolítaná a lejegyzést, túl hosszúak lennének az akkora számok, mint az évszámok, meg csak mindenki tévesztené a túl hasonló számjegyeket" Végülis ezt megválaszoltad, hisz bár a 2-es számrendszer mindennek az alapja, mégis nehézkes lenne a mindennapokban használni.
@szigetva: "Mellesleg a 12-esre se lehet, pedig annak több értelme volna" a tizenkettesre nincs értelme, mivel hosszban nem sokkal rövidülnek a számok, és bár a 2-es és utána a hármas a legfontosabb prímszám, azaz ebből a szempontból előnyös ugyan az oszthatóság megállapítása (ami fontos egy gyakran használt számrendszernél), de az öttel való oszthatóság megállapítása nehézkes, ezért helyette sokkal jobb a hatos számrendszer. A 10-esben meg ugye a 2-vel és 5-tel való oszthatóságot könnyű megállapítani, a 3-mal való oszthatóság meg még viszonylag könnyű, de mivel nem ránézésre megy (össze kell adni a számjegyeket), ezért a 10-es sem tökéletes számrendszer, de jobb, mint a 12-es.
A 6-os számrendszer viszont számtanilag jobb, mint a 10-es, ugyanis a 2-vel és 3-mal való oszthatóság megállapítása nagyon könnyű (ez ugyan a 12-esre is áll, de annak több előnye nincs), és hatosban az 5-tel való is viszonylag könnyű és 7-tel való oszthatóság megállapítása sem nehéz. Ránézésre is több számról állapítható meg, hogy nem prímszám, hisz prímszám csak 1-re és 5-re végződhet hatos számrendszerben. Érdekes módon viszont kevés nyelv használja (új-guineai törzsek, észak-afrikai törzsek és állítólag az uráli nyelvekről is azt feltételezték régebben, hogy ezt használták). A hatos számrendszer egyetlenegy hátránya, a 10-eshez képest, hogy hosszabb számokat kell leírni, viszont nem annyira zavaróan hosszúakat, mint kettesben. A 10-es nyilván a 10 ujj miatt terjedt el általánosan, azonban manapság már helyiértékesen számolunk az arab számjegyeknek hála, heyiértékes 10-es számrendszerben a 10. ujjnak nem lenne helye, hiszen helyiértékes 10-es számrendszerben 0-9.ig mennek a számjegyek, nem 1-től 10-ig.
@aphelion: "viszont helyette a 16os vagy 8as számrendszer adott esetben praktikus lehet bizonyos alkalmazásokra" a 8-as nem túl praktikus, esetleg csak informatikailag, azonban a 16-osnak több előnye is van, nemcsak informatikailag, más helyen is praktikus lenne használni, de nem megyek most inkább bele matematikailag.:-)
Ami még számtanilag jó számrendszer, az a 30-as, mert az első három prímszámmal osztható, ezáltal nagyon jó oszthatósági szabályai vannak, és tulajdonképp burkoltan sokszor használjuk is, és ez még leírható számjegyekkel, viszont a szorzótáblán sokan buknának a suliban:-) (a babiloni 60-as-ban már nehézkes lenne minden számjegynek jelet találni, 10-es számjegydeket használva meg tulajdonképp kettős számrendszert jelent)
A maják 20-as számrendszere nem olyan jól használható, mint a 10-es számrendszer. (bár a 4-gyel való oszthatóság miatt jobb, de a 3-mal való oszthatóság megállapítása rosszabb, mint a 10-esnél.
Mindent egybevéve teljesen tökéletes számrendszer nincs, a 10-es jó, de jobb sztem a 6-os, 2-es számrendszer pedig, még ha számtanilag nem is jól használható, logikai számításokhoz a legjobb. Jó még a 30-as, illetve a 16-os, és talán még a 4-es.
A többinek nem annyira van értelme, mert vagy hosszú, vagy túl sok jegy van benne, vagy nem előnyösek rá az oszthatósági szabályok stb.) Egyébként szerintem hiba, hogy csak egy számrendszert használunk (ami nem igaz, hisz ha 10-es is használunk is, sokszor burkoltan rákényszerülünk más számrendszer használatára). Aminek nincs értelme azok a páratlan számrendszerek (bár a 3-asnak és 5-ösnek lehet némi előnye néha)
81
Irgun Baklav
2018. április 16. 21:32
@arafuraferi: „30-as, mert az első három prímszámmal osztható, ezáltal nagyon jó oszthatósági szabályai vannak, és tulajdonképp burkoltan sokszor használjuk is”
Mikor használnám?
Még ha a 60-ast mondtad volna, azt az óra:perc:mp (vagy a szögek mértékegységei) esetében érteném, bár matematikai műveletet azokkal is ritkán szoktunk végezni (amikor meg mégis, akkor többnyire 10-esbe váltunk vissza).
82
szigetva
2018. április 16. 21:42
Mondjuk az egész vita teljesen akadémikus, mert még egy normális naptárreformnak (hogy a hét és az év napjai szinkronba kerüljenek) sincs esélye. De talán ez egyre kevésbé releváns is, gépekkel egyszerű a konverzió.
Az időszámítás reformja még a francia forradalomnak se sikerült.
83
arafuraferi
2018. április 16. 22:10
@Irgun Baklav: Az idő, és a kör felosztásai kevert számrendszerek, most a nem kevert számrendszerekről beszéltem. A 30-at általában olyan esetben használjuk burkoltan, amikor fontos az alapszám 3-mal való oszthatósága, de a 10-es számrendszertől sem akarunk elrugaszkodni, nem egy adott felosztásra rendszeresen, hanem esetileg használjuk. 30 60 90 120 150 mindenkinek könnyű vele számolni, de ha már szögeket említettél, épp a nevezetes szögeknek is megfelel (45-öt kivéve). De számtalan esetben kell, ha vki sokat számol.
84
Albu
2018. április 19. 23:00
Aki szerint mindegy, hogy a kört 100 vagy 360 egyenlő részre osztjuk, az számolt már valaha életében?! : ) Aki meg nem tízesben akar számolni, annak hány ujj van a két kezén? : )
85
szigetva
2018. április 20. 01:25
@Albu: Azért 10 éves kor felett sokan már nem a kezükön számolnak…
86
El Vaquero
2018. április 20. 07:34
@szigetva: annyiból egyetértek vele, hogy a 10-es számrendszernek alapjául szolgált, hogy tíz ujjunk van. Nyilván, felnőttek nem számolnak az ujjaikon, hacsak nem fogyatékosak. 2-es számrendszerben számolni is csak megszokás kérdése.
A naptárreformon én is gondolkoztam. Valami olyan felosztás kéne, aminél nincs szükség szökőévre, a hónapok egyenlő hosszúak, a napok pedig egybeesnek a csillagászati nappal. A holdciklushoz igazodás sem fontos ma már az időszámításban. Az órabeosztásnál is teljesen eltérhetnénk a 24 óra × 60 perc × 60 másodperces beosztástól, már nem kell az analóg órának körlapon mutatnia az órákat, mióta itt a digitális kor.
87
Irgun Baklav
2018. április 20. 15:49
@Albu: 12-es számrendszerben is számolhatsz az ujjaidon, a hüvelykujjaddal mutathatsz a többi ujjon lévő ujjpercekre (ezekből a hüvelykujjakat kivéve egy kézen 4*3=12 van).
www.gregapodaca.com/numerography/files/017.html
A hivatásos matemókusok komoly célokra jellemzően amúgy se a 360 fokra felosztott kört, hanem a π (pí) többszöröseit, hányadosait (pl. 30° = π/6) használják.
88
Mackósajt
2018. április 20. 18:01
@El Vaquero: "Valami olyan felosztás kéne, aminél nincs szükség szökőévre, a hónapok egyenlő hosszúak, a napok pedig egybeesnek a csillagászati nappal."
Ez nem lehetséges így együtt. Pont azért használunk szökőéveket, mert Föld keringési ciklusideje (év) nem egész számú többszöröse a Föld egyszeri körbefordulási idejének (nap). Megteheted, hogy kiiktatod a szökőévet, de akkor a napok hossza nem fog megegyezni a csillagászati nappal.
Az egyenlő hosszú hónap szintén nem lehetséges, mivel 365 (,25) napot elég nehéz egyenlő időközökre osztani. Egy megoldás, ami hirtelen eszembe jut, hogy betervezünk olyan napokat, amelyek nem részei egyetlen hónapnak sem, és akkor lehetnek egyforma hosszú hónapok (még szökőév esetén) is, de ez még rendetlenebb mint a mostani.
Ha már logikus, de soha meg nem történő, naptárreformról álmodozunk, akkor egy könnyebben megvalósítható dolog: el kéne csúsztatni az újévet úgy, hogy ténylegesen a téli napfordulóval kezdődjön az év legalább nagyjából. Elég egyszerű, csak egy évből kellene levágni a téli napforduló utáni napokat. (Más kérdés a számítógépek mit szólnának, de ott is kisebb problémának látszik, mint pl. a napok hosszának megváltoztatása.)
89
aphelion
2018. április 23. 14:03
@El Vaquero: @Mackósajt: A megoldás egyszerű: találni kell egy bolygót, aminek a keringési rátája egész számú többszöröse a fordulatszámának, lehetőleg százszorosa vagy ezerszerese vagy ilyesmi....oszt csókolom. Mármint mondani egyszerű ;)
Amíg eljutunk oda, addig viszont készüljetek, hogy egy ideig csak bonyolultabb lesz a helyzet a jelenleginél: a földi idő mellett következő lépésként külön számon tarthatjuk majd a marsi időt...
90
El Vaquero
2018. április 23. 16:29
@Irgun Baklav: ezzel anno engem beszivatott középiskolában a matektanár. Dogában kellett megoldani trigonometrikus egyenletet a valós számok halmazán. Meg is oldottam, 90° + k × 360° periódus. Erre szépen kaptam egy kövér 0 pontot. Aztán magyarázta el, hogy a feladat az volt, hogy valós számok halmazán kell megoldani. A fok egy szám utáni mértékegység, nem szám. A trigonometriailag ekvivalens π/2 + 2kπ (ahol k eleme az egész számok halmazának) az már szám, nincs mögötte semmilyen jel vagy mértékegység. Ezért számolnak a matekosok mindig radiánban, ami egy magasabb fokú absztrakció. A fok inkább egy hétköznapi fogalom, hogy az ember ne ilyen elvont π-ket lásson, hanem szögmérő meg óraszámlap segítségével el tudja képzelni a szög élességét, tompaságát is.
91
El Vaquero
2018. április 23. 16:33
@Mackósajt: én feláldozhatónak tartom a csillagászati napot. Nem baj, ha a megreformált rendszerben nem esik teljesen egybe a naptári nap a csillagászatival, év végére lesz a kettő között kb. 6 órának megfelelő különbség. Nem lenne nagyobb trauma, mint most ez az óraállítgatósdi oda-vissza. Főleg nálunk nem lenne trauma, mivel télen a nappalok úgyis rövidebbek. Az egyenlítőn meg azért lenne mindegy, mert ott meg nincs nagy különbség tél és nyár között.
Pont azért ilyen bonyolult a mostani naptár- és időszámítási rendszerünk, mert mindenféle égitest csillagászati állásának meg akar felelni.
92
aphelion
2018. április 23. 16:57
93
szigetva
2018. április 23. 17:13
@El Vaquero: Nagy mák, hogy nem vagy döntési helyzetben. Vicces lenne, hogy a végére 13:00-kor kelne a nap és éjfélkor menne le. Még szökő másodperceket is tesznek néha egy évhez, ahogy lassul a föld.
94
El Vaquero
2018. április 23. 17:48
@szigetva: igen, a szökőmásodpercekkel tisztában vagyok. Azokat meg sem lehet jósolni, hogy mikor lesz szükséges betoldani, azt csillagászok mérik le. Viszont alapvetően érdemes ezeket kiküszöbölni, amennyire csak lehet. Nyilván nem azt jelenti, hogy ezt kéne csinálni, itt most csak gondolatkísérletként írtam. De ha tudsz jobb reformot, nyugodtan írd meg. Természetesen azt sem döntési helyzettel, csak gondolati síkon. Elmélkedni ingyen van.
95
szigetva
2018. április 23. 18:09
96
Mackósajt
2018. április 23. 18:18
@aphelion: Ha a referencia szint egy pont ilyen bolygó megtalálása, elérése, és benépesítése, akkor annál talán még az is könnyebb, ha lefékezzük a Föld forgását úgy, hogy egy év egész számú nap legyen. Vagy halhatatlanná válunk, és kivárjuk, amíg a Föld forgása lelassul annyira magától, és akkor boldogok leszünk vele egy kicsit. :)
97
El Vaquero
2018. április 24. 06:49
@szigetva: igaz nem működik minden link, a lényegét nem látom annyira át, de elég nagy baromságnak tűnik. Az sem világos, hogy ez az UTC-től miben különbözik.
Volt egy olyan elképzelésem is naptárreformra, hogy a hét napjai maradnának (bár nem ártana szabványosítani, hogy a hét első napja a hétfő legyen mindenhol), de nem lennének egyáltalán hónapok. Lehet fura lenne, hogy 2029. 125., azaz pl. hogy százhuszonötödike van. A szökőévet viszont nem tudom akkor mi más módon lehetne kiküszöbölni, arra nem ajánlottál semmit, ami jobb lenne a múltkor vázolt ötletemnél.
98
szigetva
2018. április 24. 09:43
@El Vaquero: Akkor itt tobzódhatsz: en.wikipedia.org/wiki/Calendar_reform
Én nem fogok neked semmit ajánlani, mert én nem akarok naptárreformot. (A fenti linken le vannak írva a lehetőségek.) Az, hogy a hét hétfővel kezdődjön neked (meg nekem) tetszhet, másnak meg nem fog. Olyan ez, mint az univerzális világnyelv keresése: szerintem nem fog menni, viszont az AI lassan képes arra és eléggé elterjedt ahhoz, hogy fölöslegessé tegye a nyelv és az időszámítás egységesítését.
99
Akitlosz
2018. október 31. 18:11
Ezek az arabnak nevezett indiai számok akkor előnyösebbek, ha valaki tollal és papíron akar számolni.
A számoló, pláne a számítógépek korában sok előnyük már nincsen..
A római számok is jók. A valami leírásához nincsen szükség a semmi jelölésére.
A 0 római számmal N. De erre a 0 jelölésén kívül szükség nincsen.
1050 római számmal ML. Ha ez helyett azt írnák, hogy MNLN az semmivel nem nyújtana több információt, csak két felesleges extra karakter.
A római számok ma is menőbbek és előkelőbbek az arabnak nevezett indiai számoknál, amelyeknek gyakorlati előnye, ahogyan azt az elején is írtam, csak a papíron számolásnál van, de ha valaki fejben vagy géppel számol, akkor nincsen. Közönségesek.
S persze tizedesvessző használatára sincsen szükség a római számok használatával.
63,5 = LXIIIS
517,33333333333333333333333333333333333333 = DXVII....
1492,6666666666666666666666666666666666666 = MCDXCIIS..
100
Akitlosz
2018. október 31. 18:28
@Fejes László (nyest.hu):
A pontosság.
Tízes számrendszerben nem lehet pontosan ábrázolni 3 törtjeit, míg a 3 többszörösein alapuló számrendszerekben, például a hatvanas számrendszerben viszont igen.
Például 1/60-ad fok = 0,01666666666666666 fok = 1 fokperc.
10/3=3,333333333333333333333
Ugyanez 9-es számrendszerben 3,3.
S az bizony fontos tudományosan, építészetileg, hogy pontosan lehessen harmadolni, de erre a tízes számrendszer alkalmatlan.
101
Akitlosz
2018. október 31. 18:36
@tenegri:
A 10-et csak 2 felé és 5 felé lehet osztani maradék nélkül.
3 felé nem.
Ezért a 12 például jóval használhatóbb, mert azt a 2 és a 6 felé osztáson kívül 3 és 4 felé is lehet osztani maradék nélkül.
Márpedig így 60-as alapon számolni praktikusabb, mert az minden fentebb felsorolt számmal maradék nélkül osztható, és még tízzel is.
Vajon miért 12 hónap van a naptárban egy évben, amikor a valóságban 13 hónap van egy évben? A 30, 31 napos hónapok nem természetesek.
1 hónap = 28 nap = 4 hét
13X28=364.
Azért, mert a 13 prímszám, nem lehet osztani, így 13 hónap esetén nem lehet pontosan elosztani a hónapokat az évszakok, negyedévek, félévek között, míg 12 hónap esetén igen.
A 13-ik hónap különben a mercedóniusz és a február és a március között van természetesen.
102
Akitlosz
2018. október 31. 19:06
@anokó:
Csak annyit szeretnék hozzátenni, hogy a 7-es szám a Hold fázisaiból került a képbe. 1 hónapban 4 (egész) hét van. 1 hét az egy holdfázist jelöl(t), tehát természetes időtartam.
A Holdon alapuló naptár meglehetősen pontos volt a hónap háromnegyedében.
Egyszerűen mindig újholdkor volt elseje és kész. Így minden hónapban 4-ből 3 hétig pontos volt a naptár. Amíg a földművelés elterjedése miatt nem kellett a Naphoz igazodni, addig a holdnaptár, a holdév bőven megfelelő és meglehetősen pontos volt, minden egyes hónapban.hozzáigazították a valósághoz így nem csúszott el évek alatt sem.
A mai naptár sem jó még, mert nem öröknaptár. Az kinek minek jó, hogy folyton más napokra esnek a dátumok? A naptárgyártóiparnak és lobbinak, másnak nem.
Ha minden év vasárnappal kezdődne, akkor fejből lehetne tudni az összes dátumból, hogy milyen napra esik és felesleges lenne évről évre új naptárakat gyártani csak mert változik az évszám. További előny lenne, hogy minden egyes negyedév és évszak 91 napból állna ugyanannyi munkanappal, így egyszerűen összehasonlítható lenne.
A fenti követelményeket 12 és 13 hónapos naptárral is egyszerűen meg lehet oldani. A 13 hónapos naptár a radikálisabb változás, de még egyszerűbb és még praktikusabb naptárt eredményez, mert nem csupán a negyedévek napjai, de minden egyes hónap napjai is azonos napra esnének mindig. Mivel az összes hónap vasárnappal kezdődne, így mindenki azonnal tudhatná fejből, hogy 24-?, akkor az kedd, mert mindig minden 24-e kedd lenne. Míg 12 hónapos naptár esetén ez csak januárban, áprilisban, júliusban és októberben lenne így.
Az év 365-ik napja pedig "világnap" lenne, ünnepnap, amit lehetne nyugodtan hívni Szilveszternek is. Ennyi csak a trükk.
(+ szökőévenként még egy világnap június harmincadika és július elseje között.)
De "vallási okokból" ellenzik egyes országok a naptárreformot, ami már az 1950-es években is az ENSZ előtt volt.
103
Akitlosz
2018. október 31. 19:25
@El Vaquero:
Az informatikában 16-os számrendszert használnak arra, hogy a 2-es számrendszerrel működő számítógépek számai az emberek számára ne legyenek túl hosszúak. A további 6 számjegy az ABC első hat nagy betűje.
10 = A
11 = B
12 = C
13 = D
14 = E
15 = F
Tehát ami a kettesben 11111111 az FF a tizenhatosban és 255 a tízes számrendszerben.
És ennyi.
De ismertem olyan programot régen, amikor még nem volt a számítógépekben ennyire gyakorlatilag korlátlan mennyiségű memória és winchester, mint manapság, amelyik a számokat 123-as számrendszerbe számolta át és így tárolta sok tárhelyet megspórolva. A felhasználó számára persze észrevehetetlenül, ő a rendes 10-es számrendszer számait ütötte be és kapta vissza. Azért 123-as számrendszerbe, mert ennyi szám ábrázolására alkalmas különböző jelet sikerült akkoriban találni a számítógép jelei között..
104
Akitlosz
2018. október 31. 19:39
@Túlképzett Tanyasi Troll:
A 2-es számrendszer számait röviden és egyszerűen lehet ábrázolni 16-os számrendszerben.
Tehát a 20 000 az csak simán 4E20.
A 2-es számrendszer a gépeknek jó, nem az embereknek.. Minden egyes beütött internet cím is valóban csupán egy szám kettes számrendszerben, de azokat ember nem jegyezné meg, ezért vannak nevekkel helyettesítve, így az emberek számára könnyen megjegyezhető, lásd pl. nyest.hu, amivel a gép nem tudna mit kezdeni, ha nem tudná a névszervertől, hogy a
nyest. hu a kettes számrendszerben pontosan annyi mint
11000001.110.11000010.11100
Na aki ember létére ezt a számot könnyebben megjegyzi, mint azt, hogy nyest.hu neki gratulálok!
105
Kormos
2018. október 31. 19:48
@Akitlosz: "A pontosság. Tízes számrendszerben nem lehet pontosan...[mindenféle példák]...erre a tízes számrendszer alkalmatlan."
Már bocsi, de ennek semmi értelme. Annyi van, hogy az egyik számrendszer helyiérték-alapú leírásában végtelen szakaszos lehet valami, ami a másiban nem az. Ez vice versa működik egyrészt, másrészt marhára lényegtelen, mert nem csak helyiérték alapú leírás létezik. Lehet, hogy a 3,33333333333333 nem pontos annyira, mint 9-es számrendszerben a 3,3, de a ¹⁰/₃ már éppen olyan pontos. Amúgy arra is kíváncsi lennék, hogy mi az a mértékegység, amiben számolva az építészetben az általad példaként hozott 22 tizedesjegynyi pontosság számít. Talán ha megaparsecben adják meg az újságosbódé kilincsének a magasságát, még akkor sem kell annyi :D
106
Akitlosz
2018. október 31. 19:50
@arafuraferi:
A 12--es számrendszernek az a haszna, hogy a 3-mal való osztás pontosan ábrázolható benne. Na igen, cserében az 5-ttel való osztás meg nem, de legalább így jól rájöttél, hogy miért is a 60-as számot használták az ókorban és használjuk mi ma is annyi mindenhez.
Na a 60 aztán már minden fontos számmal jól osztható! 2,3,5,6,10,12!
Úgyhogy a 2 hatványai számrendszerek sem jók, csak a gépeknek, mert nem lehet pontosan ábrázolni a 3-mal való osztást 2,8,10,16-os számrendszerekben sem, pedig az tényleg fontos.
De a jövendőben lehetséges, hogy a számítógépekben egy bitnek nem csak kettő, hanem három állapota is lehetséges lesz és akkor máris majdnem minden meg lesz oldva. Na csak mert 3-as, 9-es, 27-es, 81-es számrendszerekben sem valami egyszerű számolni. :-)
Sz'al egyhamar nem lesz megúszva ez az átszámolgatásosdi.
107
Kormos
2018. október 31. 19:53
@Akitlosz: Hülyeség, bármilyen számrendszerben bármilyen osztás tökéletesen ábrázolható. Tizedestörtként nyilván nem ábrázolhatsz harmadok, de ez csak azért van, mert a harmad az nem tizedestört, hanem harmadostört. Ettől még ugyanúgy leírhatod tört alakban, és pontos lesz.
108
Akitlosz
2018. október 31. 19:58
@szigetva:
"még egy normális naptárreformnak (hogy a hét és az év napjai szinkronba kerüljenek) sincs esélye."
Ellenzik a vallási fanatikus országok. Vatikán, Amerikai Egyesült Államok. Pedig praktikus lenne és anyagi hasznot is hozna.
És a valóságot is jobban tükrözhetné, ha újra be mernék vezetni a 13-ik hónapot. Na ja az prímszám, de hát ha egyszer 13 hónap azaz Hold nap van a valóságban ...
Viszont cserében nem csupán az év, de minden hónap is szinkronba kerülne a hetekkel.
364=13X28=7X52.
Csak egyetlen nyamvadt nappal kell kezdeni valamit évente, de akkor meg úgyis mindenki ünnepel, mert éppen Szilveszter van, tehát amúgy sem sokan hívják azt a napot hétfőnek vagy éppen pénteknek, hanem Szilveszternek hívják.
109
Akitlosz
2018. október 31. 20:02
@Albu:
"még egy normális naptárreformnak (hogy a hét és az év napjai szinkronba kerüljenek) sincs esélye."
De nem kötelező, hogy minden ujj ugyanannyit jelentsen.
Ha a hüvelykujj 5-öt ér, akkor máris 18-ig tudunk számolni és mutogatni az ujjainkkal a két kezünkön.
110
Akitlosz
2018. október 31. 20:11
@El Vaquero:
Szökőévre szükség van, de ez nem gond.
13 hónapos év esetén minden hónap egyenlően 28 napos, így minden hónap elseje vasárnapra esik.
Év végén meg van egy "világnapnak" nevezett ünnepnap, a Szilveszter.
Szökőévben pedig még egy világnap június 28-a és július 1-eje között.
És ennyi.
12 hónapos év esetén pedig a január, április, július, október kezdődik vasárnappal és ezek a hónapok 31 naposak, az összes többi 30 napos. Így minden évszak és minden negyedév is egyformán 91 napból áll, ugyanannyi munkanappal - a nemzeti ünnepeket nem számolva természetesen - a Szilveszter az év végén a szökőnap pedig június 30-a és július 1-eje között.
Ez a két legjobb naptárreform javaslat szerintem.
111
Akitlosz
2018. október 31. 20:14
@Mackósajt:
"Az egyenlő hosszú hónap szintén nem lehetséges"
Simán lehetséges.
13X28=364.
A maradék egy nap pedig a "világnap" a Szilveszter, amelyik nem tartozik hónaphoz és héthez sem, csak az évhez.
Ez még több is mint lehetséges.
Annyira egyszerű, hogy az már nagyszerű.
112
Akitlosz
2018. október 31. 20:20
@Kormos:
"Már bocsi, de ennek semmi értelme. Annyi van, hogy az egyik számrendszer helyiérték-alapú leírásában végtelen szakaszos lehet valami, ami a másiban nem az. "
Akkor most semmi vagy van?
Ha magaddal sem értesz egyet, akkor előbb magaddal vitatkozzál ne velem!
Igen, az az értelme, amire magad is rájöttél, ami után én leírtam, tehát ez máris nem semmi!
113
Kormos
2018. október 31. 20:26
@Akitlosz: Magammal abszolút egyet értek. Ahogy mondtam, nem csak helyiérték alapú leírás van. Tény, hogy ha a harmadokat tizedekként próbálod leírni, végtelen szakaszos lesz, de semmi szükség másik számrendszerre ahhoz, hogy a harmadokat harmadokként írjuk le, mivel tizes számrendszerre is kész megoldásunk van arra, hogy a harmadokat harmadokként írjuk le, ez pedig pontosan az, hogy harmadokként írjuk le őket, pl.: ¹⁰/₃. Ez pedig pontosan olyan pontos, mint ha bármilyen más számrendszeren írnánk le harmadként.
114
Akitlosz
2018. október 31. 20:34
@Kormos:
"Hülyeség, bármilyen számrendszerben bármilyen osztás tökéletesen ábrázolható. Tizedestörtként nyilván nem ábrázolhatsz harmadok,"
Tehát nem hülyeség.
"de ez csak azért van, mert a harmad az nem tizedestört, hanem harmadostört. Ettől még ugyanúgy leírhatod tört alakban, és pontos lesz."
Akkor legyél szíves segítsél nekem!
Megmondanád, hogy az ⅓-ot merre találom a billentyűzeten?
A számológépé is jó. :-)
Tudsz egyáltalán írni ⅓-ot egy karakterben Controll+c, Controll+v módszer nélkül?
S akkor ez még csak az ⅓ volt, de mi van ha ⅔-ot akarnánk írni?
Na ennyire komoly és elterjedt a "harmadostörtek" használata. Még a tudományos számológépek sem ismerik. Tudományosan sem.
115
Kormos
2018. október 31. 20:38
@Akitlosz: Miért? 3,3-at tudsz írni egy karakterben?
116
Akitlosz
2018. október 31. 20:51
@Kormos:
Csak kár, hogy a számoló- sőt a számítógépek sem ismerik a módszeredet.
Leírhatod, hogy ⅓ csak ezt nem fogják számként felismerni és értelmezni sem a számoló, sem a számítógépek és nem tudnak pontosan számolni vele 2,8,10,16 stb. számrendszerekben.
Arra csak a 3, 6,9,12, 60, 360 stb. számrendszerek alkalmasak.
Na persze fel lehet tenni a kérdést, hogy minek is akkora pontosság.
Hát ha lehet valamit pontosan is kiszámolni és pontatlanul is, akkor valószínű, hogy a pontos a jobb.
Na meg aztán valamiért a pontosan ki nem számolható π értékét is egyre pontosabban akarják kiszámolni. Azt minek, hova? Az összes iskolában is elég volt csupán annyi, hogy 3,14. Akinek nem ennyivel jött ki az eredménye ő biztosan valami hű de komoly számológépet használt, amelyik pontosabban tudta. A gyakorlatban sehova sem kell olyan pontossággal, amilyen pontossággal már ismert, aztán mégis sportot űznek belőle.
Na hát az ⅓ értéke viszont pontosan ismerhető, csak nem ábrázolható pontosan tízes számrendszerben.
Számít?
Hát ha egy csokit akarunk elosztani három gyerek között ...
akkor majd kiderül.
117
Akitlosz
2018. október 31. 21:03
@Kormos:
Nem.
De, 3,3-mal lehet pontosan számolni, a gépeknek is.
Az 1/3-dal meg nem. Legalábbis 2-es, 10-es számrendszerekben nem. Ha viszont az a 3,3 9-es számrendszerben van, akkor máris pontos számot jelöl, nem kerekített.
Na persze ez nem akkora súlyú probléma, hogy akárki is ettől ne tudna aludni. Nekem megteszi a 10-es számrendszer is, a rómaiaknak is megtette. Ez a cikk nem is erről szól, hanem a számjegyekről.
Nem tűnik akkora nagy világmegváltó durranásnak ez az arabnak titulált indinai jelölésmód.
Minek tíz jel a tízes számrendszerben való számoláshoz?
Az ókori egyiptomiak is tízes számrendszert használtak, aztán mégis elegendő volt nekik ehhez 7 fajta jel is.
A lényeg, amit akartam, akarok mondani, hogy két külön dolog a számolás és a számok jelölése.
118
Kormos
2018. október 31. 21:06
@Akitlosz: Az ⅓ tökéletes pontossággal ábrázolható. Választhatsz kedvedre ⅓, 1/3, 1:3 stb. Még a számológép is ismeri, pl 1÷3 formában. A hányadosok értékét tökéleztes pontossággal megadhatjuk, tökéletes pontossággal ábrázolhatjuk, tökéletes pontossággal alkalmazhatjuk, még igazából tizedestört formában is. Akarsz egy nagy frászt? Még a 0,3̇ is tökéletesen pontos. Vagy ha jobban tetszik, 0,3̄-ként is írhatod. Mind pontos. Mind meghatározható. Mind alkalmazható. Sohasem hallottam még arról, hogy egy mérnöki probléma abból fakadt volna, hogy harmadolni kellett. Egyszerűen megteszik és kész. Tizes számrendszeren. Mivel pontosan ismerjük az értékét, nincs jelentősége annak, hogy van leírás, amiben végtelen tizedestört. Attól még ismerjük az értékét. A 60-as számrendszer sem adna semmi többet, mint a jelenleg is használt, nem végtelen leírási módok. Csak egy újabb leírási mód. Kiszámolni így is ki tudjuk, és dolgozni is tudunk vele. Semmi jelentősége annak, hogy helyiérték-alapú ábrázolásban hogy néz ki, vagy hogy nem.
119
Akitlosz
2018. október 31. 21:33
@Kormos:
Akkor jó.
Máris nyugodt vagyok.
No nem mintha, ha eddig nem az lettem volna.
120
Avatar
2018. november 6. 16:57
121
Avatar
2018. november 6. 17:23
@Akitlosz: És arra a világnapra megállna a Hold is az égen?
Mert ha nem, akkor bizony hiába mondod, hogy nem tartozik az a nap egyik hónaphoz se, a Hold bizony elkezd egy új holdhónapot.
A Hold Föld körüli keringési idejének (holdhónap) nem egész számú többszöröse a a Föld Nap körüli keringési ideje (év), sőt ezek egyike se egész számú többszöröse a Föld forgási ciklusidejének (nap), így hiába variálsz, az égbolthoz képest valahol szét fog mászni a naptár.
"A hold egy teljes ciklusának lineáris ideje 29.53059 napot tesz ki a mi megfigyelésünk szerint. Vagyis, a Hold 27.33 nap alatt kerüli meg a Földet, de a Föld is mozog a Nap körül, így összeadva a két mozgást az eredmény 29.53 nap. Ha átrágod magad a számításokon, akkor ez azt eredményezi, hogy körül-belül 12.368 megfigyelt lunáris ciklus esik egy 365.25 napos évre, de a Hold 13.36-szor kerüli meg a Földet évente."
hu.wiktionary.org/wiki/holdh%C3%B3nap