-
szigetva: @Sándorné Szatmári: Szinte mindenkinek van keze, lába, fia, lánya; kisebb számok, nap, hol...2025. 06. 30, 13:04 Mi bizonyítja, hogy a magyar nyelv finnugor?
-
Sándorné Szatmári: @szigetva: 744 Kiegészítésem: Az "alap szókincs" sem egyértelmű, mert mihez képest alap.. ...2025. 06. 30, 12:57 Mi bizonyítja, hogy a magyar nyelv finnugor?
-
Sándorné Szatmári: @szigetva: 744 Kiegészítésem: Az "alap szókincs" sem egyértelmű, mert pl. ma a "modern vil...2025. 06. 30, 12:44 Mi bizonyítja, hogy a magyar nyelv finnugor?
-
szigetva: @Sándorné Szatmári: Persze, az is lehet, hogy a Föld lapos, csak annyira elenyésző ennek a...2025. 06. 30, 11:13 Mi bizonyítja, hogy a magyar nyelv finnugor?
-
Sándorné Szatmári: @szigetva: 740 A nyelvtudomány szerintem, ahogyan 742-es hozzászólásomban írtam, nem tekin...2025. 06. 30, 10:41 Mi bizonyítja, hogy a magyar nyelv finnugor?
Kálmán László nyelvész, a nyest szerkesztőségének alapembere, a hazai nyelvtudomány és nyelvi ismeretterjesztés legendás alakjának rovata volt ez.
- Elhunyt Kálmán László, a Nyelvész, aki megmondja
- Így műveld a nyelvedet
- Utoljára a bicigliről
- Start nyelvstratégia!
- Változás és „igénytelenség”
Kálmán László korábbi cikkeit itt találja.

Ha legutóbb kimaradt, most itt az új lehetőség!
Ha ma csak egyetlen nyelvészeti kísérletben vesz részt, mindenképp ez legyen az!
Finnugor nyelvrokonság: hazugság
A határozott névelő, ami azt jelenti, hogy ‘te’
Az oroszok már a fejünkön vannak!
Míg a világ nyelveinek írásán több tucat kisebb-nagyobb írásmód osztozik ma is, addig a számjegyek írását szinte teljes mértékben a magyarul arab számok néven ismert számjegyek uralják. Korábban azonban nagyon sok írásnak saját jelölése volt a számokra is. Hogyan, hol és mikor alakultak ki, illetve minek köszönhető az arab számjegyek átütő sikere?
Az „arab”számjegyek valójában nem az araboknál alakultak ki, hanem Indiában, és az írás elterjedéséhez képest viszonylag későn. A sumerek és az egyiptomiak is nagyjából az i.e. 3. évezred közepétől már használtak írást, és a számokat is jelölték. A következő 3000 évben népek tucatjai vették át tőlük, vagy alakították ki saját írásmódjukat és számjegyek jeleit, de a ma használt számjegyek története valójában csak i.sz. 500 körül kezdődött Indiában. Természetesen a babiloni, a görög, a római és a kínai matematikusok és csillagászok is használtak számokat, de az áttörő változást csak a számok helyi érték alapú lejegyzése hozta meg.

(Forrás: wikimedia commons / Euyasik)
A helyi érték alkalmazásának különlegessége, hogy radikálisan leegyszerűsíti a matematikai műveletek végrehajtását, ami e nélkül folyamatos bonyolult átalakításokat és átszámításokat kíván. A római számokkal is lehet például szorozni és összeadni, de ehhez a jelölt számokat „konkretizálni” kellett, például abakusz segítségével. (ilyesféle eszközöket már ősidők óta ismertek). A jól működő helyi érték alapú matematika feltétele pedig a nulla, de nemcsak a nulla (latin nullus, ’semmi’) fogalma, hanem annak jelölése is.
Az oldal az ajánló után folytatódik...
A zéró fogalmáról már a fent említett kultúrákban is tudtak, de rendszeres jelölése sosem terjedt el. A maják ugyan már i.e. 36-tól használtak jelölést a nullára, ez viszont akkor nem jutott, nem juthatott el az óvilágba. Indiában azonban már legalább valamikor az i.sz. 5. századtól elkezdték használni a nulla tízes számrendszer szerinti helyi értéki jelölését. Indiai matematikusok dolgozták ki a nulla alapvető algebrai és aritmetikai alkalmazását is (Brahmagupta, 628). Az indiai számokat és használatukat vette át a perzsa származású Abu Abdalláh Muhammad ibn Músza al-Hvárizmi (i.sz. 780 – 845).
Al-Hvárizmi Bagdadban élt és arab nyelven írta műveit. Bagdadban jelent meg A Számítás hindu számokkal című munkája is 825 körül, és ezzel az „arab” számok visszafordíthatatlanul elindultak hódítóútjukon. Nevéhez nemcsak ez, hanem az algebra és az algoritmus szavak származása is köthető, az előbbi egyik könyvcímének, az utóbbi pedig saját nevének rövidítéséből és latinosításából került be az európai nyelvekbe az első latin nyelvű fordítás után (1145). Maga a zéró szó szintén arab eredetű, a صفر ṣifr, ’üres’ szó olasz változata honosult meg különböző módokon az európai nyelvekben. (Az arab kifejezés egyébként pedig a szanszkrit sunya fordítása.)
A nagyon jó kulturális kapcsolatokkal rendelkező arab világ tudósai között gyorsan terjedt az új számjelölés, a távolsággal és az idővel azonban kicsit megváltoztak a számok formái. A hindu-arab számokként is ismert jelöléseknek három fontosabb változata létezik ma is: az indiai, a keleti arab és a nyugati arab. Európába e legutóbbi érkezett el, melyeket a 976-os kiadású Codex Vigilanus említ először.
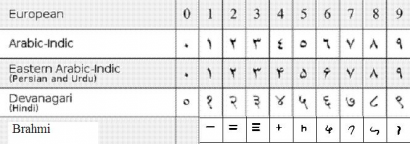
(Forrás: wikimedia commons, nyest)
Az új számjegyek európai meghonosodása lassú folyamat volt. A következő lökést a számjegyeket Észak-Afrikában elsajátító olasz matematikus, Leonardo Fibonacci 1202-ben kiadott Liber Abaci című könyve adta, de az általános elterjedés csak a nyomatatás feltalálása után – Gutenberg, c. 1440 – gyorsult fel. Angliában például 1445-ben, Magyarországon pedig V. László (1440-1457) rövid uralkodásának végén jelentek meg az arab számok először. Oroszország a 18. század végén, Nagy Péter uralkodása alatt, Kína és Japán pedig a 19. század végén kezdte el használni az arab számjegyeket. Ma már szinte minden ország és nyelv alapvetően a hindu-arab számokat használja, azoknak is túlnyomórészt az általunk is ismert nyugati arab változatát. Ez alól kivételt csak azok a nyelvterületek képeznek, ahonnan a nyugati arab számok korábbi változata történelmileg származik, tehát főleg az arab országok és India kulturális hatókörzete.
Ez utóbbi területhez főleg Dél-Ázsia és Délkelet-Ázsia tartozik, ahol sok nyelv a bráhmi családba tartozó saját írásmódot használ. Az indiai nyelveken kívül ilyen még például a burmai, a thai, a lao, és a khmer is. Ezek a nyelvek nem csak bráhmi írásra visszavezethető írásjelekkel rendelkeznek, de többségüknek saját, a hindu-arabhoz hasonló, helyi érték alapú számjegyeik is vannak. Ugyan ma már az európai számjegyek is általánosan ismertek ezeken a területeken is, de a hagyományos helyi számjegyek használta is él még. Például e nyelvek wikipédia szócikkei is gyakran a hagyományos számjegyeket használják, és a bankjegyek előlapján is gyakran találkozhatunk ilyen európaiak számára „felismerhetetlen" számokkal.

(Forrás: wikimedia commons)
A hindi nyelvű wikipédia is a dévanágari számokat használja, de az indiai bankjegyeken már csak a nyugati arab számok jelennek meg, pont azért, mert az indiai nyelvek többségének saját számjegyei vannak. A dévanágari számjegyekkel is találkozhatunk azért bankjegyeken, például a nepáli rúpiákon.
Az arab világban a számjegyek használata nem teljesen egységes. Egyiptomtól nyugatra az Európában is ismert nyugati arab számjegyek jellemzőek, a többi területen viszont a keleti arab számjegyek az általánosan elterjedtek. Ez a különbség az térség bankjegyeinek számjegyeiben is megmutatkozik. A keleti arab államok papírpénzének előlapján a keleti arab számjegyek szerepelnek, és csak a hátoldalukon láthatóak az európaiak számára is könnyen felismerhető nyugati arab számjegyek, míg Egyiptomtól nyugatra már a bankjegyeken is csak az utóbbi számokkal találkozhatunk.
A fent említett példák ellenére az arab számjegyek sikere szinte teljesnek mondható, és alapvetően a logikusságuknak, praktikusságuknak köszönhető.
Olvasói kérésre itt egy táblázat a számjegyek európai fejlődéséről:

Források:
http://mathforum.org/dr.math/faq/faq.roman.html#calc
http://www.omniglot.com/language/numerals.htm
http://www.skypoint.com/members/waltzmn/Mathematics.html