A neurális hálók egyidősek a számítógépekkel. Arról, hogy milyen számítási feladatokat lehet megoldani velük, élénk vitákat tudnak folytatni a kutatók. A viták lényege, hogy ha egy jelenség tanulható, akkor formalizálható, azaz leírható egy függvénnyel. Ezen most elég annyit értenünk, hogy adott bemeneti (input) értékekhez adott kimeneti (output) értéket rendel egy függvény. Ezeket gyakran nagyon nehéz leírni, a neurális hálók ellenben a tanulás során ezeket közelítik.

Macska a hálóban

A legelterjedtebb módszer szerint a háló mesterséges neuronjai között véletlenszerűek a kapcsolatok erősségei. Amikor elkezdjük tanítani a hálózatot, folyamatosan bemutatjuk neki a tanító halmazt, ami cserébe minden körben a hibái tükrében igazít a neuronok közötti kapcsolatokon. Így anélkül hogy ismernénk a bemenetek és kimenetek közötti függvényt, annak egyre jobb közelítését kapjuk.

Minsky és Papert 1969-ben megjelent Perceptrons című könyve rendesen odavágott a neurális hálók világának, hiszen bebizonyította, hogy az egyszerű hálózatok nagyon sok függvényt képtelenek közelíteni. Annyira népszerű volt bizonyításuk, hogy a nyolcvanas években a könyv leporolt változata újra megjelent, de ekkor már többen is dolgoztak a problémán és 1989-ben majd 1991-ben Cybenko és Hornik kutatásainak hála megszületett az úgynevezett univerzális közelítés tétele, mely szerint a megfelelő architektúrával rendelkező neurális hálók a legtöbb függvényt képesek jól közelíteni. De továbbra is égető kérdés, hogy hogyan is lehetséges ez!

Forrás: http://arxiv.org/pdf/1608.08225v1.pdf

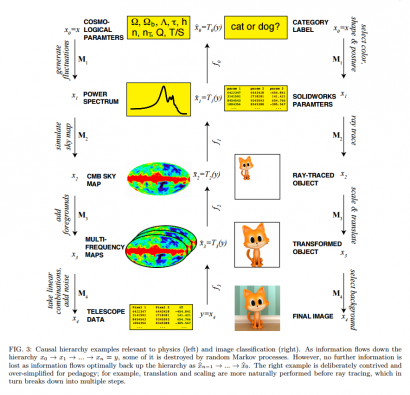
Lin és Tegmark az arXiv preprint szerveren megjelent tanulmánya szerint a neurális hálók szerencsések, mert a legtöbb természeti jelenséget viszonylag egyszerű szabályok (függvények!) működtetik. Ezért a neurális hálóknak nem végtelen sok lehetséges függvényt kell közelíteniük, hanem csupán pár darab jöhet szóba minden megoldandó probléma esetén. Ha például egy egy megabájtos fekete-fehér képről kellene megmondanunk, hogy egy macskát ábrázol-e, akkor azzal szembesülhetünk, hogy a kép minden pixele 256 különböző értéket vehet fel, azaz összesen kb. 256 az egymilliomodik hatványon különböző kép lehetséges, amiről döntenünk kell.

Ezt elvileg leírhatjuk egy függvényben, ami minden lehetséges pixel kombinációhoz hozzárendeli a „macska” ill. a „nem macska” címkét. A neurális hálók azonban sokkal egyszerűbben – az összes lehetséges adat csupán töredékét használva! – közelítik egészen jól ezt a függvényt. Ennek oka az, hogy nem is kell végigmenni a pixelek összes lehetséges kombinációján, hiszen a fizika törvényeinek hála a cicának és minden másnak is csupán ezek kis százaléka látszhat.

Az oldal az ajánló után folytatódik...

Mivel a fizikai világot viszonylag pár egyszerű alapvető törvény írja le, a neurális hálóknak nem kell végigtalálgatniuk az összes lehetséges állapotot, az inputok és a hozzájuk rendelhető outputok erősen behatároltak. Például, ha egy cicát elforgatunk 90 fokkal, akkor a cica ugyanaz a cica marad, ha távolabbról nézzük (vagy fotózzuk), akkor pedig méretarányosan kisebb lesz, de alapvető tulajdonságai nem változnak. Azaz a cicákban van valami invariáns, nem változó dolog, ami a különféle átalakulások, transzformációk során is állandó marad.

Jó tudni, hogy a cicás képek osztályozásában lehet számítani a neurális hálók segítségére. Azt azonban továbbra sem tudjuk, hogy a nem természeti jelenségekre, azaz az ember alkotta társadalmi jelenségekre is alkalmazhatóak-e a neurális hálók. De ez már egy másik történet.